Surface Area of a Rectangular Pyramid Calculator
Table of contents
Surface area of a rectangular pyramidExample: Using the surface area of rectangular pyramid calculator.Other rectangular pyramid calculatorsFAQsUse this surface area of a rectangular pyramid calculator to deal with rectangular pyramids. Whether rectangular or square, these kinds of pyramids are famously associated with history across the globe! Be it the Egyptian pyramids or the Latin American ones. Pyramids are not just monuments but are also useful in determining the hardness of materials! The Vickers hardness test uses a pyramid indenter for that purpose. This article will explain how you can calculate its surface area.
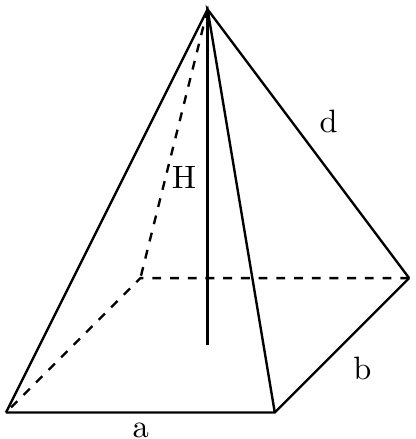
Surface area of a rectangular pyramid
The total surface area of a rectangular pyramid () is the sum of two areas:
- The area of the base; and
- The area 4 surrounding triangles, otherwise known as the lateral surface area.
Consider a rectangular pyramid with the following dimensions:
- a - Base length;
- b - Width of the base; and
- H - Height of the pyramid.
Now, the area of the base () is a rather simple calculation. It is the area of a rectangle, i.e.
Whereas, you can calculate the lateral surface area as an area of a triangle. If the slant heights are and , for the respective sides, the lateral surface area is given by the equation:
You can write the slant heights in the form of height and base length of the pyramid. Such that the lateral surface area becomes:
Example: Using the surface area of rectangular pyramid calculator.
Find the surface area of a rectangular pyramid having base dimensions as 4 and 5 cm. Take the height of the pyramid as 5 cm.
To find the surface area:
- Enter the length of the base as
5 cm. - Insert the width of the base as
4 cm. - Fill in the height of the pyramid as
5 cm. - The surface area of a rectangular pyramid calculator will return the area as:
Advanced mode
You can enable the additional values section to view the slant height and face areas of the pyramids.
Other rectangular pyramid calculators
There are other tools based on rectangular pyramids that you can refer to learn more cool things about this omnipresent shape, such as:
- Right rectangular pyramid calculator;
- Rectangular pyramid volume calculator;
- Pyramid volume calculator;
- Pyamid angle calculator;
- Square pyramid calculator;
- Square pyramid volume calculator;
- Right square pyramid calc;
- Height of a square pyramid calculator; and
- Surface area of a square pyramid calculator.
How do I calculate the slant height of the rectangular pyramid?
To calculate the slant height of the rectangular pyramid:
- Find the square of the base length of the pyramid.
- Divide the square by
4. - Add the resultant with the square of the height of the pyramid.
- Find the square root of the sum to obtain the slant height of the pyramid.
- Repeat the steps with the base width to find the other slant height.
How do I calculate the lateral surface area of a rectangular pyramid?
To calculate the lateral surface area of a rectangular pyramid:
- Find the slant heights of the pyramid.
- Multiply slant height with the base length of the pyramid.
- Repeat step 2 with the base width.
- Add the two areas to obtain the lateral surface area of the pyramid.
What is the surface area of a pyramid with base length 4 cm and height 6 cm?
The surface area of the pyramid is 66.6 sq. cm. Out of which, the 50.6 sq. cm is the lateral surface area, which is calculated as: 2 × 4 × √((0.25×16) + 36) = 50.6 sq. cm., while 16 sq. cm is the base area.
