Square Pyramid Volume Calculator

This square pyramid volume calculator will help you learn:

• how to find the volume of a right square pyramid,
• the different square pyramid volume formulas, and
• the measurements you can and cannot use to find a square pyramid's volume.

This volume of a pyramid with a square base calculator is easy to use and comes with explanations and instructions to help you with your square pyramid volume calculations. Keep on reading to start learning 🙂!

To find the volume of a pyramid with a square base, this calculator will be your best friend. All you need to do is enter any two measurements of your square pyramid into our calculator. Once you've done that, our calculator will then provide you with the volume of your square pyramid 🙂.

In the next section of this text, we'll discuss the different square pyramid formulas we used to make this volume of a pyramid with a square base calculator work.

The formula we use to find the volume of a square pyramid only uses two variables that we can easily measure on a pyramid. Those measurements are the base edge (a) and the height (H) of the pyramid, shown in the image below:

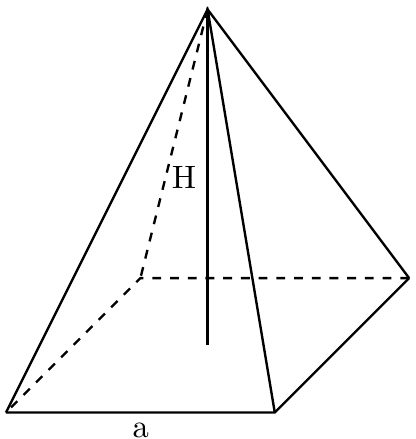
With those measurements, we can then calculate the volume of the square pyramid (V) with the help of this formula:

We can quickly determine a square pyramid's volume using the aforementioned formula. However, sometimes, we cannot measure $a$ or $H$, say something obstructs us from doing so. But instead, we can measure or have at least one of the values for the slant height ($s$) and lateral edge ($d$), shown in the image below:

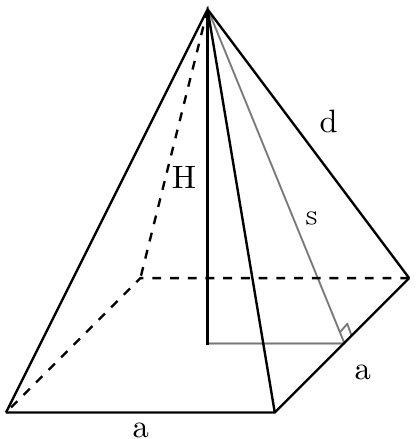
In those cases, we can utilize the Pythagorean Theorem to express $a$ in terms of $s$ or $d$ and $H$ in terms of $a$ and $s$. Then we can derive and use one of these square pyramid volume formulas, depending on the measurements we know:

If we don't know $H$:

• $V = a^2 \times \frac{\sqrt{s^2 - (a / 2)^2}}{3}$

• $V = a^2 \times \frac{\sqrt{\frac{d^2 - a^2}{2}}}{3}$

If we don't know $a$:

• $V = 4 \times (s^2 - H^2) \times \frac{H}{3}$

• $V = 4 \times (d^2 - s^2) \times \frac{H}{3}$

• $V = 2 \times (d^2 - H^2) \times \frac{H}{3}$

If you want to learn more about finding a square pyramid's height, you can check out our height of a square pyramid calculator.

In some other scenarios, we may lack the measurements mentioned above to quickly find a square pyramid's volume. Good thing we can derive those measurements using the different surface areas of our pyramid, as shown in this image:

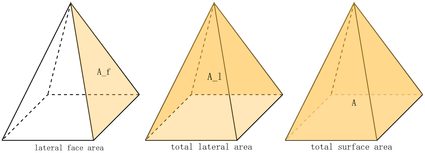
We can find the slant height using the lateral face area if we know our pyramid's base edge. The same goes for the total lateral area, which is simply the lateral face area multiplied by four. You can learn more about these surface areas and the formulas that you can use to derive $a$, $s$, or $H$ in our right square pyramid calculator.

Craving for more pyramid-related calculations and knowledge? Here are some of our other cool calculators you can check out 🙂:

• Right rectangular pyramid calculator
• Pyramid volume calculator
• Square pyramid calculator
• Right square pyramid calc
• Height of a square pyramid calculator
• Surface area of a square pyramid calculator
• Rectangular pyramid volume calculator
• Surface area of a rectangular pyramid calculator