Absolute Value Calculator

In this absolute value calculator, we provide all of the necessary information about the absolute value function and its inequalities, and, obviously, we help you calculate the absolute value of any number. To help you understand better what an absolute value is, we have included some absolute value graphs and a few practical examples of solving absolute value equations. So come in and enjoy learning new things about absolute value!

Let's start from the beginning, shall we? The term absolute value might have different meanings, depending on the context, but here, in the mathematical world, it is very clearly defined. The absolute value definition is simply the value of the number, regardless of the sign. This absolute value definition is not the most technical one, but it's sure to confuse no one while explaining what absolute value is.

For those who like more technicality when it comes to their mathematical definitions, we haven't forgotten about you:

The absolute value, or modulus |x|, of a real number x is the non-negative value of x without regard to its sign. Namely, |x| = x for a positive x, |x| = −x for a negative x (in which case −x is positive), and |0| = 0.

Now that you know what absolute value is, we can talk about how to write it and operate with it in mathematical terms. The mathematical symbol for absolute value is |x|, where x would denote whatever number we want the absolute value of. For example, the absolute value of 3 is written as |3| while the absolute value of -5.3 would be written as |-5.3|.

To calculate the absolute value of a number, you simply "take the sign off" of the number. One can also think about it as "making the number inside positive." If you want to sound fancier, you can always make up your own way to explain, depending on what you'd like to compute. For example, "you find the distance between the number you're interested in and the value 0 (zero)".

It is important to know that the absolute value operation is not just limited to numbers. It can be applied to expressions and equations like this: |-3x + 3| where x would be an unknown value.

We will explain later how to calculate the absolute value of equations or the absolute value of a graph/function. For now, let's go step by step.

You bet it is!

Oh! I guess you want some reasons and examples of what is absolute value useful for, right? Well, let's start with the easiest: any situation in which we care about differences and only differences. For example, when we are talking about the distance between two things. The obvious one is the distance between two points, which is, for example, necessary alongside time when calculating speed.

For example, if a car starts at x = 5 and moves to x = 2, how far has it traveled? You can simply say it's 5 - 2 = 3, but that is technically incorrect since the distance is actually the absolute value of the difference between the starting finish and the finishing point. In this case, the equation to solve this would be |2 - 5| = |-3| = 3, which gives us the same result as before but much more technical prowess to show off ;)

We can also use the absolute value as a way of abbreviating our writing. For example, if we want a function that gives only positive numbers, we could write a set of 'if...else' conditions, but that would get too long. This is where absolute value comes to the rescue: we can simply wrap our function inside the absolute value signs to give us permanent positive values. This means that |f(x)| is always positive no matter the value of f(x).

And this usefulness leads directly to absolute value graphs and absolute values inside of functions. Both are simple things in theory, but both are tricky in the beginning.

Let's start with the most basic absolute value function: f(x) = |x|. Before we think about its shape, we already know that this absolute value function can only have values above and on the x-axis; that is, f(x) only has positive and zero values.

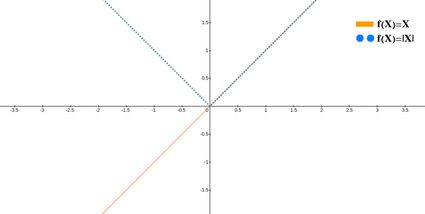
Digging a bit deeper, we can start with the positive part, x > 0. In this case, f(x) = x, so we get a straight line at exactly 45º which bisects the first graph quadrant of the Cartesian plane. The part for negative x, x < 0, can be rewritten as f(x) = -x, which gives a line symmetrical to the positive x part with the y-axis acting as the axis of symmetry. This part bisects the second quadrant and forms an angle of 135º with the x-axis. For the sake of completeness, we should add that f(0) = |0| = 0, completing the symmetry.

Things get a bit more sophisticated when we get a more complicated expression inside the absolute value. As long as the absolute value surrounds the whole expression, we can use a small trick. If we look back at f(x) = |x| as a modification on f(x) = x, we can see that the difference is that the negative part of f(x) = x has been altered to have positive values. More precisely, what we've done is flipped it around the x-axis so that it is now a mirror image of the original part.

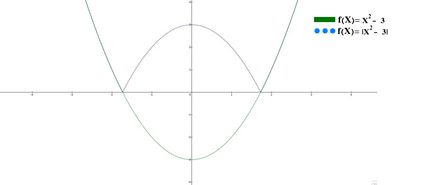
This same trick can be used for any absolute value function. Just draw the function ignoring the absolute value, and then flip over whatever part is below y = 0, which you can calculate using our slope intercept form calculator. The result is a perfect representation of the absolute value graph without any headaches.

As a side note for those interested, any absolute value graph is as continuous as the non-absolute one, but will also have a sharp, non-differentiable point wherever the values have begun to change from positive to negative. For example, in the function f(x) = |x|, we get a sharp point at f(0) = 0.

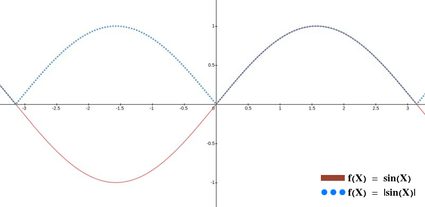
For more complicated expressions where the absolute value function is inside the expression (like in f(x) = 2x + 3 / |x|), things get more complicated and require more thorough mathematical analysis. It is not impossible to do, and it's more about labor than complexity. However, that goes beyond the scope of this calculator, so we will stop here and swiftly move on to absolute value equations and inequalities.

A common place to find absolute values is when solving absolute value equations (or any kind of equation, really). Equations that have absolute values are known as absolute value equations; if instead of an equals (=) sign, we have a greater than (>), less than (<), greater than, or equal to (≥), or less than or equal to (≤) sign, then we have what is called an absolute value inequality.

The way to deal with absolute values in both cases is similar. When solving absolute value equations, you want to operate on and simplify things as much as possible while avoiding touching the absolute value part until you absolutely (pun intended) have to.

Once we hit the point where we need to deal with the absolute value, we isolate it on one side of the sign and decompose it into its possible options: positives and negatives. This process is the same for both absolute value equations and absolute value inequalities.

Let's see how that would look with a very simple example. Imagine you've managed to simplify everything to the point where you have the following equation:

4x + 1 = |2x - 3|

We know that the part |2x - 3| is always going to be positive but 2x - 3 could be positive OR negative. If it's positive, the equation would be:

4x + 1 = 2x - 3

while it is negative, the absolute value would change the sign, giving us the following:

4x + 1 = -(2x - 3) => 4x + 1 = 3 - 2x

Both equations represent potential solutions of the initial equation and would yield:

a) Positive: x = -2
b) Negative: x = 1/3

If we pay close attention we can see that we are not done, since x = -2 means that 2x - 3 = -4 - 3 = -7. As the result is a negative number, this violates the assumption we made that |2x - 3| > 0, so we know that x = -2 cannot be a solution. This is confirmed if we check this:

4·(-2) + 1 = |2·(-2) - 3| => -8 + 1 = |-4 - 3| => -7 = +7,

which is a mathematical absurdity.

This same process of dividing the absolute value equation or absolute value inequality, then checking what solutions make sense, is very useful and standard. You can use it when solving any absolute value equation (even if it's a quadratic formula), and your success is pretty much guaranteed.

We used a very simple example here to keep it brief. Still, the same techniques can be used to solve very complex inequalities or find important points in absolute value functions so that you can draw the absolute value graphs we mentioned earlier.

Using the absolute value calculator is as easy as it gets. As a mathematical operation, the absolute value is very easy to find in and of itself, but we're going to try and talk you through a couple of tips that might help you.

First of all, the absolute value calculator works by turning any number you input into a positive number, which is all the absolute value really is. So you should introduce a number in the input box of the calculator, and you will get its absolute value as a result.

You can use this tool to check certain points of your absolute value graph and equation to make that sure your sketch, drawing, or solution is correct.

It is a very simple calculator, and that is why we have provided all the information above: to turn this simple absolute value calculator into a tool to gain more knowledge, bound to be helpful in your life (or at least in your math class).