Reference Angle Calculator

Our reference angle calculator is a handy tool for recalculating angles into their acute version. All you have to do is simply input any positive angle into the field, and this calculator will find the reference angle for you. This article explains what a reference angle is, providing a reference angle definition.

It will also provide you with a step-by-step guide on how to find a reference angle in radians and degrees, along with a few examples. Keep scrolling, and you'll find a graph with quadrants as well!

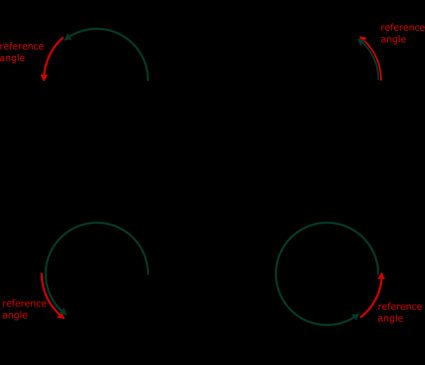
Look at the picture above. Every angle is measured from the positive part of the x-axis to its terminal line (the line that determines the end of the angle) traveling counterclockwise. If you want to find the reference angle, you have to find the smallest possible angle formed by the x-axis and the terminal line, going either clockwise or counterclockwise.

Reference angles are useful in trigonometry. If you want to find the sine or cosine of any arbitrary angle, you first have to look for its reference angle in the first quarter. Then you can find the trigonometric function of the reference angle and choose a proper sign.

The most commonly used angles and their trigonometric functions can be found in the table below:

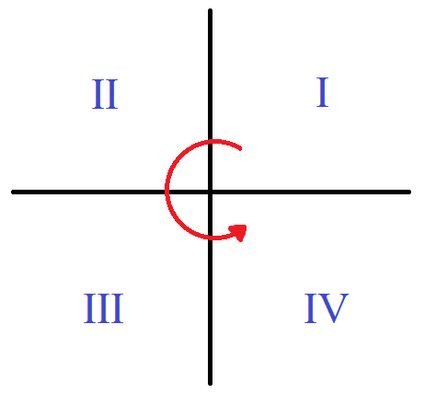
The two axes of a 2D Cartesian system divide the plane into four infinite regions called quadrants. Numbering starts from the upper right quadrant, where both coordinates are positive, and goes in an anti-clockwise direction, as in the picture.

Generally, trigonometric functions (sine, cosine, tangent, cotangent) give the same value for both an angle and its reference angle. The only thing that changes is the sign — these functions are positive and negative in various quadrants. Follow the "All Students Take Calculus" mnemonic rule (ASTC) to remember when these functions are positive.

• A for all: in the first quadrant, all trigonometric functions have positive values.
• S for sine: in the second quadrant, only the sine function has positive values.
• T for tangent: in the third quadrant, tangent and cotangent have positive values.
• C for cosine: in the fourth quadrant, only the cosine function has positive values.

If you don't like this rule, here are a few other mnemonics for you to remember:

• All Stations To Central 🚆
• Add Sugar To Coffee ☕
• All Science Teachers (are) Crazy 👩‍🏫

Make sure to take a look at our law of cosines calculator and our law of sines calculator for more information about trigonometry.

All you have to do is follow these steps:

1. Choose your initial angle — for example, 610°.

2. If your angle is larger than 360° (a full angle), subtract 360°. Keep doing it until you get an angle smaller than a full angle. This is the same as finding the modulo. In this example, after subtracting 360°, we get 250°.

3. Determine in which quadrant does your angle lie:

   • 0° to 90° — first quadrant,
   • 90° to 180° — second quadrant,
   • 180° to 270° — third quadrant,
   • 270° to 360° — fourth quadrant.

   In this case, 250° lies in the third quadrant.

4. Choose the proper formula for calculating the reference angle:

   • 0° to 90°: reference angle = angle,
   • 90° to 180°: reference angle = 180° − angle,
   • 180° to 270°: reference angle = angle − 180°,
   • 270° to 360°: reference angle = 360° − angle.

   In this case, we need to choose the formula reference angle = angle − 180°.

5. Substitute your angle into the equation to find the reference angle:

   reference angle = 250° − 180° = 70°.

If you need a tool to help convert between different units of angle measurements, try out our angle conversion.

It's easier than it looks!

1. For angles larger than 2π, subtract multiples of 2π until you are left with a value smaller than a full angle.
2. Determine the quadrants:

• 0 to π/2 — First quadrant, so reference angle = angle;
• π/2 to π — Second quadrant, so reference angle = π − angle;
• π to 3π/2 — Third quadrant, so reference angle = angle − π; and
• 3π/2 to 2π — Fourth quadrant, so reference angle = 2π − angle.

As you can see, this procedure is similar to the one above for degrees. As an example, let's consider the angle of 28π/9 radians.

1. Having subtracted the multiples of 2π, we're left with 10π/9.

2. 10π/9 is a bit more than π, so it lies in the third quadrant. The reference angle is:

   reference angle = angle - π = π/9

It couldn't be easier! Simply:

1. Type the angle into the box. It may be any positive angle you imagine; let's say we want to find the reference angle for 210°. If you wish, you may also change the units, e.g., to radians.
2. That's it! This reference angle calculator found the acute version of your angle as well as the quadrant in which your initial angle lies. It's 30° in our case, and the initial angle lies in the third quadrant. Awesome!

If you want a quick answer, have a look at the list below:

First quadrant:

Second quadrant:

Third quadrant:

Fourth quadrant: