Law of Cosines Calculator

The law of cosines calculator can help you solve a vast number of triangular problems. You will learn what is the law of cosines (also known as the cosine rule), the law of cosines formula, and its applications. Scroll down to find out when and how to use the law of cosines, and check out the proofs of this law. Thanks to this triangle calculator, you will be able to find the properties of any arbitrary triangle quickly.

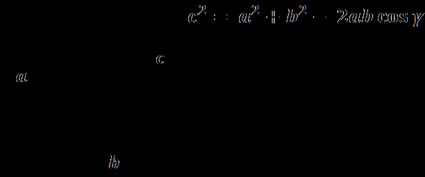
But if, somehow, you're wondering what the heck is cosine, better have a look at our cosine calculator.

The law of cosines states that, for a triangle with sides and angles denoted with symbols as illustrated above,

a² = b² + c² - 2bc × cos(α)

b² = a² + c² - 2ac × cos(β)

c² = a² + b² - 2ab × cos(γ)

For a right triangle, the angle gamma, which is the angle between legs a and b, is equal to 90°. The cosine of 90° = 0, so in that special case, the law of cosines formula is reduced to the well-known equation of Pythagorean theorem:

a² = b² + c² - 2bc × cos(90°)

a² = b² + c²

The law of cosines (alternatively the cosine formula or cosine rule) describes the relationship between the lengths of a triangle's sides and the cosine of its angles. It can be applied to all triangles, not only the right triangles. This law generalizes the Pythagorean theorem, as it allows you to calculate the length of one of the sides, given you know the length of both the other sides and the angle between them.

The law appeared in Euclid's Element, a mathematical treatise containing definitions, postulates, and geometry theorems. Euclid didn't formulate it in the way we learn it today, as the concept of cosine had not been developed yet.

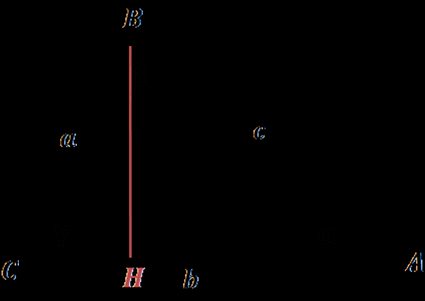
AB² = CA² + CB² − 2 × CA × CH (for acute angles)

AB² = CA² + CB² + 2 × CA × CH (for obtuse angles)

However, we may reformulate Euclid's theorem easily to the current cosine formula form:

CH = CB × cos(γ), so AB² = CA² + CB² - 2 × CA × (CB × cos(γ))

Changing notation, we obtain the familiar expression:

c² = a² + b² - 2ab × cos(γ)

The first explicit equation of the cosine rule was presented by Persian mathematician d'Al-Kashi in the 15th century. In the 16th century, the law was popularized by the famous French mathematician Viète before it received its final shape in the 19th century.

You can transform these law of cosines formulas to solve some problems of triangulation (solving a triangle). You can use them to find:

1. The third side of a triangle, knowing two sides and the angle between them (SAS):

   • a = √[b² + c² - 2bc × cos(α)]

   • b = √[a² + c² - 2ac × cos(β)]

   • c = √[a² + b² - 2ab × cos(γ)]

2. The angles of a triangle, knowing all three sides (SSS):

   • α = arccos [(b² + c² - a²)/(2bc)]

   • β = arccos [(a² + c² - b²)/(2ac)]

   • γ = arccos [(a² + b² - c²)/(2ab)]

3. The third side of a triangle, knowing two sides and an angle opposite to one of them (SSA):

   • a = b × cos(γ) ± √[c² - b² × sin²(γ)]

   • b = c × cos(α) ± √[a² - c² × sin²(α)]

   • c = a × cos(β) ± √[b² - a² × sin²(β)]

Just remember that knowing two sides and an adjacent angle can yield two distinct possible triangles (or one or zero positive solutions, depending on the given data). That's why we've decided to implement SAS and SSS in this tool, but not SSA.

The law of cosines is one of the basic laws, and it's widely used for many geometric problems. We also take advantage of that law in many Omnitools, to mention only a few:

• Triangle angle calculator
• Triangle area calculator
• Perimeter of a triangle calculator
• Triangular prism calculator

Also, you can combine the law of cosines calculator with the law of sines to solve other problems, for example, finding the side of the triangle, given two of the angles and one side (AAS and ASA).

There are many ways in which you can prove the law of cosines equation. You've already read about one of them – it comes directly from Euclid's formulation of the law and an application of the Pythagorean theorem. You can write the other proofs of the law of cosines using:

1. Trigonometry

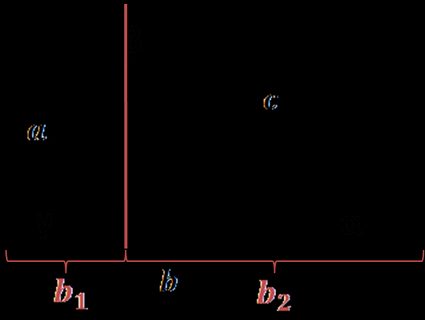
Draw a line for the height of the triangle and divide the side perpendicular to it into two parts:

b = b₁ + b₂

From sine and cosine definitions, b₁ might be expressed as a × cos(γ) and b₂ = c × cos(α). Hence:

b = a × cos(γ) + c × cos(α) and by multiplying it by b, we get:

b² = ab × cos(γ) + bc × cos(α) (1)

Analogical equations may be derived for other two sides:

a² = ac × cos(β) + ab × cos(γ) (2)

c² = bc × cos(α) + ac × cos(β) (3)

To finish the law of cosines proof, you need to add the equation (1) and (2) and subtract (3):

a² + b² - c² = ac × cos(β) + ab × cos(γ) + bc × cos(α) + ab × cos(γ) - bc × cos(α) - ac × cos(β)

Reduction and simplification of the equation give one of the forms of the cosine rule:

a² + b² - c² = 2ab × cos(γ)

c² = a² + b² - 2ab × cos(γ)

By changing the order in which they are added and subtracted, you can derive the other law of cosine formulas.

2. Distance formula

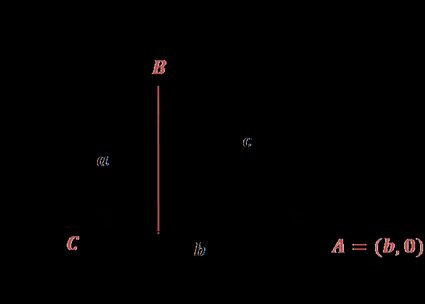
Let C = (0,0), A = (b,0), as in the image.

To find the coordinates of B, we can use the definition of sine and cosine:

B = (a × cos(γ), a × sin(γ))

From the distance formula, we can find that:

c = √[(x₂ - x₁)² + (y₂ - y₁)²] = √[(a × cos(γ) - b)² + (a × sin(γ) - 0)²]

Thus:

c² = a² × cos(γ)² - 2ab × cos(γ) + b² + a² × sin(γ)²

c² = b² + a²(sin(γ)² + cos(γ)²) - 2ab × cos(γ)

As a sum of squares of sine and cosine is equal to 1, we obtain the final formula:

c² = a² + b² - 2ab × cos(γ)

3. Ptolemy's theorem

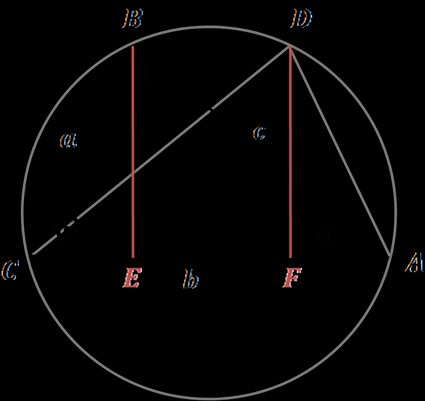
Another law of cosines proof that is relatively easy to understand uses Ptolemy's theorem:

• Assume we have the triangle ABC drawn in its circumcircle, as in the picture.

• Construct the congruent triangle ADC, where AD = BC and DC = BA

• The heights from points B and D split the base AC by E and F, respectively. CE equals FA.

• From the cosine definition, we can express CE as a × cos(γ).

• Thus, we can write that BD = EF = AC - 2 × CE = b - 2 × a × cos(γ).

• Then, for our quadrilateral ADBC, we can use Ptolemy's theorem, which explains the relation between the four sides and two diagonals. The theorem states that for cyclic quadrilaterals, the sum of products of opposite sides is equal to the product of the two diagonals:

  BC × DA + CA × BD = AB × CD

  so in our case:

  a² + b × (b - 2 × a × cos(γ)) + a² = c²

• After reduction, we get the final formula:

  c² = a² + b² - 2ab × cos(γ)

The great advantage of these three proofs is their universality – they work for acute, right, and obtuse triangles.

4. Using the law of sines
5. Using the definition of dot product
6. Comparison of areas
7. Geometry of the circle

The last two proofs require the distinction between different triangle cases. The one based on the definition of dot product is shown in another article, and the proof using the law of sines is quite complicated, so we have decided not to reproduce it here. If you're curious about these law of cosines proofs, check out the Wikipedia explanation.

1. Start with formulating your problem. For example, you may know two sides of the triangle and the angle between them and are looking for the remaining side.

2. Input the known values into the appropriate boxes of this triangle calculator. Remember to double-check with the figure above whether you denoted the sides and angles with correct symbols.

3. Watch our law of cosines calculator perform all the calculations for you!

If your task is to find the angles of a triangle given all three sides, all you need to do is to use the transformed cosine rule formulas:

α = arccos [(b² + c² - a²)/(2bc)]
β = arccos [(a² + c² - b²)/(2ac)]
γ = arccos [(a² + b² - c²)/(2ab)]

Let's calculate one of the angles. Assume we have a = 4 in, b = 5 in and c = 6 in. We'll use the first equation to find α:

α = arccos [(b² + c² - a²)/(2bc)]

= arccos [(5² + 6² - 4²)/(2 × 5 × 6)]

= arccos [(25 + 36 - 16)/60]

= arccos [(45/60)] = arccos [0.75]

α = 41.41°

You may calculate the second angle from the second equation in an analogical way, and the third angle you can find by knowing that the sum of the angles in a triangle is equal to 180° (π).

If you want to save some time, type the side lengths into our law of cosines calculator - our tool is a safe bet! Just follow these simple steps:

1. Choose the option depending on given values. We need to pick the second option – SSS (3 sides).

2. Enter the known values. Type the sides: a = 4 in, b = 5 in, and c = 6 in.

3. The calculator displays the result! In our case the angles are equal to α = 41.41°, β = 55.77° and γ = 82.82°.

After such an explanation, we're sure that you understand what the law of cosine is and when to use it. Give this tool a try, solve some exercises, and remember that practice makes permanent!