Cosine Calculator
This cosine calculator is a twin tool to our sine calculator – add to them the tangent calculator, and you'll have a pack of the most popular trigonometric functions. Simply type the angle – in degrees or radians – and you'll find the cosine value instantly.
Read on to understand what is a cosine and to find the cosine definition, as well as a neat table with cosine values for basic angles, such as cos 0°, cos 30°, or cos 45°.
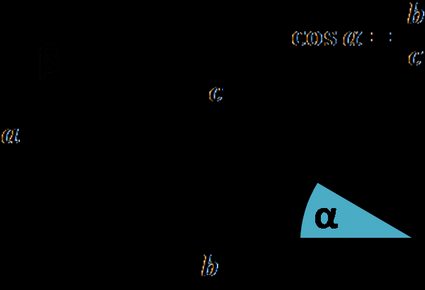
What is cosine? Cosine definition
Cosine is one of the most basic trigonometric functions. It may be defined based on a right triangle or unit circle, in an analogical way as the sine is defined:
The cosine of an angle is the length of the adjacent side divided by the length of the hypotenuse.
cos(α) = adjacent / hypotenuse = b / c
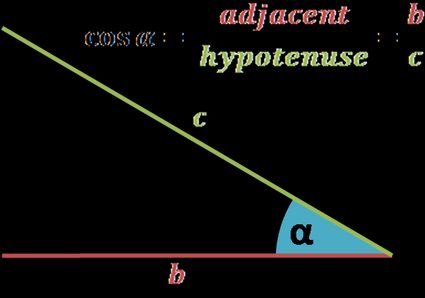
If you're not sure what the adjacent and hypotenuse are (and opposite, as well), check out the explanation in the sine calculator (link at the top of this article).
The name cosine comes from the Latin prefix co- and sine function – so it literally means sine complement. And, indeed, the cosine function may be defined that way: as the sine of the complementary angle – the other non-right angle. The abbreviation of cosine is cos, e.g., cos(30°).
Important properties of a cosine function:
- Range (codomain) of a cosine is -1 ≤ cos(α) ≤ 1;
- Cosine period is equal to 2π;
- It's an even function (while sine is odd!), which means that cos(-α) = cos(α); and
- Cosine definition is essential to understand the law of cosines – a very useful law to solve any triangle. Discover it with our law of cosines calculator!

Cosine graph and table (cos 0, cos 30 degrees, cos 45 degrees...)
The image below shows the cosine function in <-2π, 2π> range. Also, if you'd like to learn how to play around with it, make sure to check the phase shift calculator.
The exact cosine value is particularly easy to remember and to define for certain angles – you probably learned that cos 0° = 1, cos 30° = √3/2, or cos 45° = √2/2. Other basic angles are shown in the table:
α (angle) | sin(α) | ||
|---|---|---|---|
Degrees | Radians | Exact | Decimal |
0° | 0 | 1 | 1 |
15° | π/12 | (√6 + √2) / 4 | 0.9659258263 |
30° | π/6 | √3/2 | 0.8660254038 |
45° | π/4 | √2/2 | 0.7071067812 |
60° | π/3 | 0.5 | 0.5 |
75° | 5π/12 | (√6 - √2) / 4 | 0.2588190451 |
90° | π/2 | 0 | 0 |
105° | 7π/12 | -(√6 - √2) / 4 | -0.2588190451 |
120° | 2π/3 | -0.5 | -0.5 |
135° | 3π/4 | -√2/2 | -0.7071067812 |
150° | 5π/6 | -√3/2 | -0.8660254038 |
165° | 11π/12 | -(√6 + √2) / 4 | -0.9659258263 |
180° | π | -1 | -1 |
Moreover, you can observe how the cosine function behaves according to the quadrant in which it lays. Remember the periodicity of the cosine function cos(α + 360°) = cos(α) if your angle is not shown in the table below.
Quadrant / Border | Degrees | Radians | Value | Sign | Monotony | Convexity |
|---|---|---|---|---|---|---|
0° | 0 | 1 | Maximum | |||
1st Quadrant | 0° < α < 90° | 0 < α < π/2 | 0 < cos(α) < 1 | + | Decreasing | Concave |
90° | π/2 | 0 | Root, inflection | |||
2nd Quadrant | 90° < α < 180° | π/2 < α < π | -1 < cos(α) < 0 | - | Decreasing | Convex |
180° | π | -1 | Minimum | |||
3rd Quadrant | 180° < α < 270° | π < α < 3π/2 | -1 < sin(α) < 0 | - | Increasing | Convex |
270° | 3π/2 | 0 | Root, inflection | |||
4th Quadrant | 270° < α < 360° | 3π/2 < α < 2π | 0 < sin(α) < 1 | + | Increasing | Concave |
Example: how to use a cosine calculator
Now you got the hang of what is cosine; using this cosine calculator is a piece of cake!
-
Enter the angle. Switch between the units with a simple click on the unit name. Let's take 40° as an example.
-
Keep calm and read the result – in our case, cos(40°) ≈ 0.766 (remember, it's an approximate value; an exact cosine value can be found only for specific cases).
Give this cosine calculator a go! Play around by typing the cosine value and finding the angle. The only thing to notice is that our tool will show you the angles in 0-180° range – as you know about the periodicity and that the cosine is an even function, it shouldn't be a problem for you to find other possible solutions.