Phase Shift Calculator
Welcome to Omni's phase shift calculator, where we'll study trigonometric functions and how to calculate their phase shift. In fact, we'll cover more than that: we'll also explain how to find the amplitude and how to find the period. As a matter of fact, it turns out that a huge class of functions behave virtually the same, and the differences boil down to describing the very values mentioned above; the amplitude, period, and phase shift. Well, up to a vertical shift, at least.
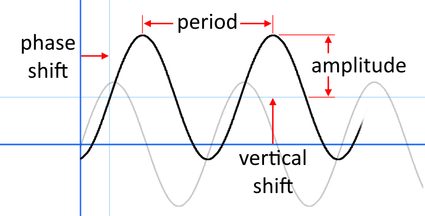
The amplitude, period, phase shift, and vertical shift
As we've mentioned above, we'll be focusing here on trigonometric functions: more specifically on the sine and cosine. Nevertheless, it's important to remember that many of the notions are more general, especially those of the horizontal translation or the vertical shift.
First of all, let's look at a picture showing where the amplitude, period, phase shift, and vertical shift appear on the graph (note that the same image appears at the top of Omni's phase shift calculator).
We can write such functions with the formula (sometimes called the phase shift equation or the phase shift formula):
or:
where , , , are arbitrary real numbers, but with and non-zero (otherwise, it wouldn't be a trigonometric function). Obviously, those four numbers determine the amplitude, period, phase shift, and vertical shift. To an extent, the picture suggests how they affect the graph. Still, it'd be useful to support the visuals with some definitions.
-
The amplitude is how far (either way) the values run from the graph's centerline. For a simple sine or cosine, its value is since the centerline is at , and the function's values range from to .
-
The period is the length on the horizontal axis, after which the function begins repeating itself. In other words, the (infinite) graph is just a bunch of period-length copies glued together at the ends. For a simple sine or cosine, the period equals since and the parts in between are exactly the same (and similarly for the cosine).
-
The phase shift (also called the horizontal shift or horizontal translation) describes how far horizontally the graph has been moved from the regular sine or cosine. As such, the value is equal to if we have the two functions unaltered.
-
The vertical shift (also called the vertical translation) describes how far vertically the graph has been moved from the regular sine or cosine. In other words, it's the phase shift's twin that concerns the perpendicular direction. In particular, the value is again equal to if we have the two functions unaltered.
Alright, we've learned what the phase shift is, as well as the three accompanying values. The sections below describe how to calculate each of them based on the notation from the phase shift formula above. First, we show how to find the amplitude.
The concept we introduced is widespread in the study of oscillatory and harmonic motions. To say it all, those phenomena are best buddies with trigonometry. You can discover the connection at our trigonometry calculator or learn more about the various functions that keep popping up when you analyze a pendulum at the trigonometric functions calculator — or the more specific cosine calculator and sine calculator!
How to find the amplitude
We know that the sine and cosine functions have values ranging from to . What is more, that simple fact doesn't change if we substitute or for or for a non-zero and arbitrary . In fact, it's because the function is then a bijection (i.e., a one-to-one correspondence) onto the space of real numbers.
Now let's see what happens if we add , i.e., if we have or instead. Since the first part gives something between and , the whole thing will be between and (see How to find the vertical shift for comparison). That means the centerline falls at , and the amplitude is still because the values fall as far as away from .
Therefore, the only thing that can affect the amplitude in the phase shift formulas and is the non-zero . And indeed, since and are all this time between and , the multiplier changes this range to and .
Yup, you guessed it: the amplitude of the phase shift equations and is simply equal to .
How to find the period
Recall that the sine and cosine functions have periods equal to , i.e., we have and for any . In particular, that gives:
and:
So, we see that the and in the phase shift formula have no effect on the period. Indeed, it all boils down to what happens inside the trigonometric functions. And yet:
and:
By the very same rules as above, so it's not the either that does the job. So, with three options discarded, it must be the fourth: the .
We again turn to the comment we started with to understand why and how affects periodicity in the phase shift equations and . After all:
So with every added to the argument , we land back in the same spot, and the function repeats itself (and similarly for the cosine).
All in all, the period of a phase shift equation is equal to .
Our daily knowledge of waves usually prioritizes the frequency over the period; however, they are almost the same thing. Discover why at Omni's frequency calculator.
How to find the phase shift
By definition, the phase shift describes the horizontal translation of the function with respect to the regular or . As such, the basic functions have it equal to . In fact, if we compare their graphs:
…we'll notice that we can get one by translating the other (in fact, mutual cofunctions have many similarities). To be precise, we have the following:
and:
The example above already suggests where in and , we should look for the values responsible for phase shifts. However, as opposed to the amplitude and period, this time, we'll need two of the four letters.
In general, (that is, not only in phase shift equations), we obtain the horizontal translation of an arbitrary function by calculating : the shift of the graph by to the right. In other words, we substitute every occurrence of with in the formula for . For instance, applying the translation to gives , but for, say, we'd get:
In other words, we cannot forget about the multipliers standing in front of .
In our case, the phase shift formula gives:
which is a phase shift of (to the right) of the function . Of course, we can repeat the above for the cosine as well.
To sum it all up, in order to calculate the phase shift of a phase shift equation, you need to find .
How to find the vertical shift
This one's easy, especially now that we've seen what the phase shift, amplitude, and period are and how to calculate them. Let us build on what we've learned so far.
We know that in the phase shift formulas and , the determines how far the values fluctuate on either side of the centerline. The specifies how far we extend the graph's bumps and, as a result, how fast we get to repeat the values. Also, together with , the two describe if we've moved the function to the left or right and how much.
Obviously, the horizontal translation doesn't affect the vertical shift: those are two perpendicular directions, after all. On the other hand, the amplitude only tells us how far vertically the graph reaches but it doesn't shift it. All in all, we're left with only one letter: .
The in the phase shift equations is precisely the vertical shift. It determines the function's range, i.e., how far from the usual, no- version we move the graph.
That concludes the theoretical part for today. It's time to see how to calculate the phase shift on a nice example. And you know what? We'll show how to find the period, the amplitude, and the vertical shift as well. After all, why not? More mathematical calculation = more fun!
Example: using the amplitude period phase shift calculator
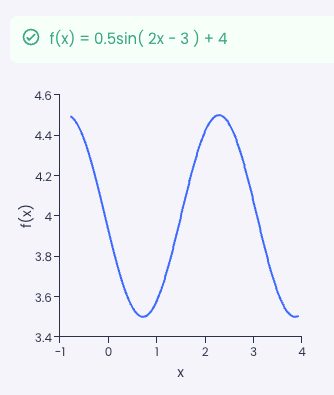
Let's see how to find the amplitude, period, phase shift, and vertical shift of the function . Firstly, we'll let Omni's phase shift calculator do the talking.
At the top of our tool, we need to choose the function that appears in our formula. In our case, we choose "sine" under "The trigonometric function in f." That'll trigger a symbolic representation of such a phase shift equation: . Looking back at what we have, we input the following:
The moment we give the last value, the function's graph appears underneath together with the amplitude, period, phase shift, and vertical shift further down. Also, observe that if needed, you can use the option "Calculate f(x) at a point", located at the bottom of the calculator, to find the function's value at any point .
Now let's explain how to find the phase shift and all the other values ourselves. For that, it's enough to recall the four sections above to calculate that:
- The amplitude is ;
- The period is ;
- The phase shift is ; and
- The vertical shift is .
All in all, the graph looks like this:
A piece of cake, wasn't it? Make sure to play around with the phase shift calculator to see how different coefficients affect the graph.
FAQs
How do I calculate the phase shift?
To calculate the phase shift of a function of the form A × sin(Bx - C) + D or A × cos(Bx - C) + D, you need to:
- Determine
B. - Determine
C. - Divide
C/B. - Remember that if the result is:
- Positive, the graph is shifted to the right.
- Negative, the graph is shifted to the left.
- Enjoy having found the phase shift.
How do I find the phase shift from a graph?
To find the phase shift from a graph, you need to:
- Determine whether it's a shifted sine or cosine.
- Look at the graph to the right of the vertical axis.
- Find the first:
- Peak if the coefficient before the function is positive; or
- Trough if the coefficient is negative.
- Calculate the distance from the vertical line to that point.
- If the function was a sine, subtract
π/2or3π/2from that distance for a peak or a trough, respectively. - Enjoy having found the phase shift from a graph.
How do I find the amplitude, period, and phase shift?
Finding the amplitude, period, and phase shift of a function of the form A × sin(Bx - C) + D or A × cos(Bx - C) + D goes as follows:
- The amplitude is equal to
A; - The period is equal to
2π / B; and - The phase shift is equal to
C / B.
How do I graph trig functions with phase shift?
To graph trig functions with phase shift, you need to:
- Determine what the trig function is.
- Focus on the point
(0,0)on the plane. - If the phase shift is:
- Positive, move to the right.
- Negative, move to the left.
- Move the distance given by the phase shift.
- The point you land in is your starting point.
- Draw the non-shifted function's graph as if the point were
(0,0). - Enjoy having graphed a trig function with a phase shift.
Are horizontal and phase shift the same?
When it comes to trigonometric functions, yes. We usually reserve the term "phase shift" for trig functions. In other words, we can have a horizontal shift of any graph or function. Still, when it is, in fact, a trigonometric one, we can equivalently call that horizontal shift a phase shift.