Trigonometric Functions Calculator

This trigonometric functions calculator can help in determining the values of six trig functions in no time. You'll find here not only the three basic functions – sine, cosine and tangent, but also their reciprocals: cosecant, secant and cotangent, respectively.

Scroll down to read more about trigonometric ratios, find sin cos tan charts and learn the mnemonic rule to remember function definitions – sohcahtoa. Don't wait any longer. Give this trigonometric functions calculator a try!

Sine, cosine, and tangent are the trigonometric functions of an angle. If the angle is acute, you can define these trig functions in the context of a right triangle. Starting with the triangle sides nomenclature: we can name the sides of a right triangle as

• Hypotenuse – you've probably heard this term when learning about the Pythagorean theorem. So it's the longest side in the right triangle – the opposite one to the right angle (90°).

• Adjacent side – the side forming the angle of interest (in our case, angle α), which is not a hypotenuse. This side is adjacent to both the angle of interest and the right angle.

• Opposite side – the side opposite to the angle of interest (in this case, angle α).

Given the sides definitions, you can state that:

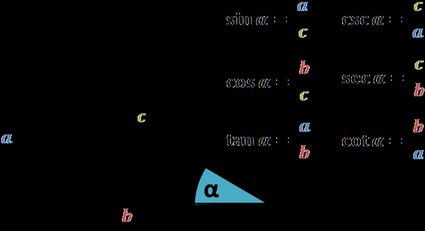
sin(α) = opposite / hypotenuse so sin(α) = a / c

cos(α) = adjacent / hypotenuse so cos(α) = b / c

tan(α) = opposite / adjacent so tan(α) = a / b

If you want to read more about those three famous functions, jump directly to our dedicated tools:

• Sine calculator;
• Cosine calculator; and
• Tangent calculator.

But if you don't care too much about the details and just want to calculate all functions at once, use this tool as a complete sin cos tan calculator.

In the previous section, you learned about basic trigonometric ratios:

But what if we would like to invert the ratios? Like c / a instead of a / c? Apparently, these reciprocal trigonometric ratios have their own names and are even used sometimes! So, for the right triangle:

1. Cosecant is the reciprocal of the sine

   It's the ratio of the hypotenuse to the opposite side. The abbreviation of cosecant is csc, e.g., csc(30°) and it's range is csc(α)≥ 1 and csc(α) ≤ -1:

   csc(α) = 1 / sin(α) = c / a

2. Secant is the reciprocal of the cosine

   It's the ratio of the hypotenuse to the adjacent. The abbreviation of secant is sec, e.g., sec(30°) and it's range is sec(α)≥ 1 and sec(α) ≤ -1:

   sec(α) = 1 / cos(α) = c / b

3. Cotangent is the reciprocal of the tangent

   It's the ratio of the adjacent to the opposite side. The abbreviation of cotangent is cot, e.g., cot(30°) and it's range is -∞ < cot(α) < ∞:

   cot(α) = 1 / tan(α) = b / a

If you think that's all trigonometric ratios there are (the six above) – you're wrong! There are many other trig functions – like, e.g., hacoversine, exsecant, or versine – but, fortunately, they are archaic and obsolete, so they are not used nowadays. If you want to read more about those trigonometric functions used in dark pre-calculators ages, check out this post by Evelyn Lamb from Scientific American Blog.

Maybe you heard about that helpful sohcahtoa ("soak-a-toe", "sock-a-toa", "so-kah-toa") mnemonic?

• SOH stands for Sine equals Opposite over Hypotenuse.

• CAH stands for Cosine equals Adjacent over Hypotenuse.

• TOA stands for Tangent equals Opposite over Adjacent.

It's one of the methods to remember the definition of the basic trigonometric functions, but many other techniques exist. For example, you can simply pick one sentence which appeals to you the most:

• Sailors Often Have Curly Auburn Hair Till Old Age ⛵

• Some Old Horses Can Always Hear Their Owners Approach 🐎

• Some Old Hen Caught Another Hen Taking One Away 🐔

• Studying Our Homework Can Always Help To Obtain Achievement 📖

• Some Old Hippy Caught Another Hippy Tripping On Acid ☮️

Or invent your own! They are always the easiest to remember!

The trigonometric functions can also be defined in terms of the rise, run, and slope of a line segment relative to horizontal.

Below you'll find the sin, cos, and tan charts for the range <-2π, 2π>, as well as graphs for their reciprocal functions. And if you'd like to learn to play around with the shapes, make sure to check the phase shift calculator.

• Sine:

• Cosine:

• Tangent:

And their reciprocal counterparts:

• Cosecant:

• Secant:

• Cotangent:

Are you still wondering how to use this trigonometric functions calculator? Don't worry; it's a piece of cake! 🍰

1. Enter the angle. Choose between degrees and radians (in two versions, rad or π rad). Let's take π/3 as an example, so choose π rad unit and type 1/3.

2. Here it is! Six trig functions calculated by the trigonometric functions calculator in the blink of an eye! And also an explanatory image if the angle is acute. What more can you ask, right?

Now that you have explored six trigonometric functions, you might have fallen in love with trigonometry and want to dive deeper into the subject. For that, we recommend checking out the Computer Technology For Math Excellence's webpage. This a great collection of resources to help you improve your math knowledge and understanding.

Or maybe you've had enough trigonometry for today, and you're ready for more advanced topics, such as law of sines and law of cosines.