Omni Calculator logo
Last updated:

Trig Identities Calculator

New

Table of contents

What are trig identities?The first trig identity: the Pythagorean identityCalculate trig identities for rotations and reflectionsVerify and calculate trig identities for composite, multiple, and half anglesHow to use Omni's trig identities calculatorFAQs

Our trig identities calculator takes any angle as input and lets you explore the trigonometric identities that use its value. You will meet double and half angles, compositions, rotation, and more. Keep reading to learn:

  • What are trig identities? A brief introduction to the mathematical language of the tool;
  • The trig identities in right triangles;
  • The effect of rotations and reflections on the trig functions; and
  • How to calculate and verify trig identities for double angles (and much more).

This tool covers most of the necessary things to know when tackling trigonometry and is a valuable ally to refresh those pesky formulas!

What are trig identities?

Trig identities are a class of mathematical identities applied to trigonometric functions. They are instrumental when dealing with angles and often help you calculate the values of trigonometric functions of otherwise hard-to-find angles.

🙋 An identity is a mathematical equality that compares two properties or functions (mathematical expressions). Identities are valid in specific ranges of values. It differs from a simple equation since the latter involves unknowns and their values.

The first trig identity: the Pythagorean identity

The Pythagorean identity shows the deep connection between trigonometry and right triangles. Starting from the unit circle, we can see how sine and cosine are the legs of a right triangle with hypotenuse equal to the radius. Our right triangle trigonometry calculator can make this connection even clearer.

The formula that relates sine and cosine is a simple version of Pythagora's theorem: it assumes the form of the following identity.

sin⁡2(θ)+cos⁡2(θ)=1\footnotesize\sin^2(\theta) + \cos^2(\theta) = 1

You can compute sine and cosine by isolating them from the equation before:

cos⁡(θ)=±1−sin⁡2(θ)sin⁡(θ)=±1−cos⁡2(θ)\footnotesize\begin{split} \cos(\theta) &= \pm\sqrt{1 - \sin^2(\theta)}\\[1em] \sin(\theta) &= \pm\sqrt{1 - \cos^2(\theta)} \end{split}

Notice how we introduced a plus-minus sign: for each value of the sine, we can identify two possible values of the cosine, and vice-versa.

Calculate trig identities for rotations and reflections

Since the trig functions are defined on a circle, as you can see in our trigonometric functions calculator, we can easily identify two transformations of these functions. Let's learn how to calculate the trig identities in the case of rotations and reflections.

Verify and calculate trig identities for rotations

Trigonometric functions are periodic around a circle (or a fraction of it): we can define rotations using fractions of the period. Our calculator implements three of those:

  • Quarter of the period (π2\frac{\pi}{2});
  • Half of the period (π\pi); and
  • Full periods (k×πk\times\pi).

In the table below, you can see the various identities for the three most important trig functions:

Shift by quarter of the period

Shift by half of the period

Shift by full periods

sin⁡(θ±π2)=±cos⁡(θ)\sin\left(\theta \pm \frac{\pi}{2}\right)=\pm\cos(\theta)

sin⁡(θ±π)=−sin⁡(θ)\sin\left(\theta\pm\pi\right) = - \sin(\theta)

sin⁡(θ±k⋅2π)=sin⁡(θ)\sin\left(\theta \pm k\cdot2\pi\right) = \sin(\theta)

cos⁡(θ±π2)=∓sin⁡(θ)\cos\left(\theta \pm \frac{\pi}{2}\right)=\mp\sin(\theta)

cos⁡(θ±π)=−cos⁡θ)\cos\left(\theta\pm\pi\right) = - \cos\theta)

cos⁡(θ±k⋅2π)=cos⁡(θ)\cos\left(\theta \pm k\cdot2\pi\right) = \cos(\theta)

tan⁡(θ±π4)=tan⁡(θ)±11∓tan⁡(θ)\tan\left(\theta \pm \frac{\pi}{4}\right)=\frac{\tan(\theta)\pm1}{1\mp\tan(\theta)}

tan⁡(θ±π2)=−cot⁡(θ)\tan\left(\theta\pm\frac{\pi}{2}\right) = - \cot(\theta)

tan⁡(θ±k⋅π)=tan⁡(θ)\tan\left(\theta \pm k\cdot\pi\right) = \tan(\theta)

Note that the period of the tangent is only π\pi, and not 2π2\pi as for sine and cosine. You can use the above trig identities to verify this: calculate the tangent for the angle θ\theta and the angle θ+π\theta + \pi, and you will see that they equal each other!

tan⁡(θ+π)=sin⁡(θ+π)cos⁡(θ+π)=−sin⁡(θ)−cos⁡(θ)=sin⁡(θ)cos⁡(θ)=tan⁡(θ)\footnotesize\begin{split} \tan(\theta + \pi) &= \frac{\sin(\theta+\pi)}{\cos(\theta+\pi)} \\[1em] &= \frac{-\sin(\theta)}{-\cos(\theta)} = \frac{\sin(\theta)}{\cos(\theta)}\\[1em] & = \tan(\theta) \end{split}

Calculate the trig identities for reflections

The periodic behavior of the trig functions can be used to define identities according to reflections with respect to lines at certain angles (α\alpha). In this tool, we will explore reflections for:

  • The horizontal axis (α=0\alpha = 0);
  • The bisector of the first quadrant (α=45°=π/4\alpha = 45\degree = \pi/4);
  • The vertical axis (α=90°=π/2\alpha = 90\degree = \pi/2); and
  • The bisector of the second quadrant (α=135°=3π/4\alpha = 135\degree = 3\pi/4).

We can define these reflections also by the effect they have on the angle:

  • α=0\alpha = 0 implies θ→−θ\theta \rightarrow -\theta;
  • α=45°=π/4\alpha = 45\degree = \pi/4 implies θ→π/2−θ\theta \rightarrow \pi/2 - \theta;
  • α=90°=π/2\alpha = 90\degree = \pi/2) implies θ→π−θ\theta \rightarrow \pi-\theta; and
  • α=135°=3π/4\alpha = 135\degree = 3\pi/4 implies θ→3π/2−θ\theta\rightarrow 3\pi/2 - \theta.

α=0\boldsymbol{\alpha = 0}

α=45°=π/4\boldsymbol{\alpha = 45\degree = \pi/4}

α=90°=π/2\boldsymbol{\alpha = 90\degree = \pi/2}

α=135°=3π/4\boldsymbol{\alpha = 135\degree = 3\pi/4}

sin⁡(−θ)=−sin⁡(θ)\sin(-\theta) = -\sin(\theta)

sin⁡(π2−θ)=cos⁡(θ)\sin\left(\frac{\pi}{2}-\theta\right) = \cos(\theta)

sin⁡(π−θ)=sin⁡(θ)\sin(\pi-\theta) = \sin(\theta)

sin⁡(3π2−θ)=−cos⁡(θ)\sin\left(\frac{3\pi}{2}-\theta\right) = -\cos(\theta)

cos⁡(−θ)=cos⁡(θ)\cos(-\theta) = \cos(\theta)

cos⁡(π2−θ)=sin⁡(θ)\cos\left(\frac{\pi}{2}-\theta\right) = \sin(\theta)

cos⁡(π−θ)=−cos⁡(θ)\cos(\pi-\theta) = -\cos(\theta)

cos⁡(3π2−θ)=−sin⁡(θ)\cos\left(\frac{3\pi}{2}-\theta\right) = -\sin(\theta)

tan⁡(−θ)=−tan⁡(θ)\tan(-\theta) = -\tan(\theta)

tan⁡(π2−θ)=cot⁡(θ)\tan\left(\frac{\pi}{2}-\theta\right) = \cot(\theta)

tan⁡(π−θ)=−tan⁡(θ)\tan(\pi-\theta) = -\tan(\theta)

tan⁡(3π2−θ)=cot⁡(θ)\tan\left(\frac{3\pi}{2}-\theta\right) = \cot(\theta)

🙋 Note that by combining reflections and shifts, we can identify many other identities. However, the tools we gave you here are more than enough to start!

Verify and calculate trig identities for composite, multiple, and half angles

The last category of trig identities we will study in this tool involves composition and multiplication of angles. The trig identities you'll verify and calculate in this section will help you find the values of trigonometric functions for "exotic" angles outside of the ones you usually remember.

Calculate the trig identities for the composite angle

The composite angle identity is the only one we will analyze that considers two angles: we will see how their sum and difference are always directly connected to the value of the trigonometric functions for the individual angles.

Before even introducing the mathematical formula, we will give you a graphical interpretation of these identities, and trust us: it's pure genius!

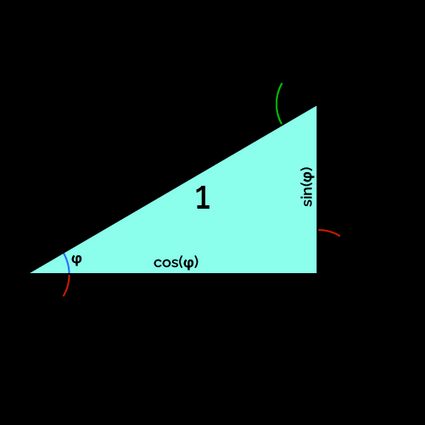
A depiction of the composite angle identities

Start by tracing a right triangle with hypotenuse 11, and call one of the angles φ\varphi. Using the relationship between right triangles and trigonometric function, you can easily find the length of the sides (sin⁡(φ)\sin(\varphi) and cos⁡(φ)\cos(\varphi)). Now add another right triangle below the original one, with the hypotenuse equal to the side cos⁡(φ)\cos(\varphi) of the original triangle. Call the corresponding angle θ\theta, and calculate the sides: hint: it suffices to multiply the sine and cosine of θ\theta by the hypotenuse (cos⁡(φ)\cos(\varphi)). Repeat the steps above for the similar triangle built on the other side of the original triangle.

Eventually, we apply the property of parallel lines and identify the last right triangle with the acute angle (θ+φ\theta+\varphi). This triangle shares the hypotenuse with the original one, so its sides are simply cos⁡(θ+φ)\cos(\theta+\varphi) and sin⁡(θ+φ)\sin(\theta+\varphi).

Since we created a rectangle, we can compare the results and find the desired identities. Here are the formulas that you can see from the picture above.

sin⁡(θ±φ)=sin⁡(θ)cos⁡(φ)±cos⁡(θ)sin⁡(φ)cos⁡(θ±φ)=cos⁡(θ)cos⁡(φ)∓sin⁡(θ)sin⁡(φ)\footnotesize \begin{split} \sin(\theta\!\pm\!\varphi) &\!=\! \sin(\theta)\cos(\varphi)\!\pm\!\cos(\theta)\sin(\varphi)\\[1em] \cos(\theta\!\pm\!\varphi) & \!=\!\cos(\theta)\cos(\varphi)\!\mp\!\sin(\theta)\sin(\varphi) \end{split}

This formula is the starting point for other, more elegant identities. Let's discover them!

Calculate trig identities for the double and triple angle

What happens when we substitute φ=θ\varphi=\theta in the identities above? We'd find double-angle identities. These are handy formulas, and it's worth spending some time on them. Let's analyze the double angle formula for the sine.

Take the identity above, sin⁡(θ ⁣+ ⁣φ) ⁣= ⁣sin⁡(θ)cos⁡(φ) ⁣+ ⁣cos⁡(θ)sin⁡(φ)\small \sin(\theta\!+\!\varphi) \!=\! \sin(\theta)\cos(\varphi)\!+\!\cos(\theta)\sin(\varphi), and perform the substitution φ=θ\varphi=\theta :

sin⁡(θ+θ)=sin⁡(2θ)=sin⁡(θ)cos⁡(θ)+cos⁡(θ)sin⁡(θ)=2sin⁡(θ)cos⁡(θ)\footnotesize \begin{split} \sin(\theta\!+\!\theta) &\!=\!\sin(2\theta)\\[.5em] &\!=\! \sin(\theta)\cos(\theta)\!+\!\cos(\theta)\sin(\theta)\\[.5em] &\!=\!2\sin(\theta)\cos(\theta) \end{split}

🙋 There are other ways to express this identity: discover them at the double angle identities calculator!

For the cosine, the reasoning is the same: let's see the formula right away:

cos⁡(θ+θ)=cos⁡(2θ)=cos⁡(θ)cos⁡(θ)−sin⁡(θ)sin⁡(θ)=cos⁡2(θ)−sin⁡2(θ)\footnotesize \begin{split} \cos(\theta\!+\!\theta) &\!=\!\cos(2\theta)\\[.5em] &\!=\! \cos(\theta)\cos(\theta)\!-\!\sin(\theta)\sin(\theta)\\[.5em] &\!=\!\cos^2(\theta)\!-\!\sin^2(\theta) \end{split}

To calculate the trig identity for the tangent's double angle, we would need to

Composite and double angle identities for the tangent

The tangent lacks the elegance of the sine and the cosine when it comes to composite and double angles (but we still love it). Here is the formula for the composite angle:

tan⁡(θ+φ)=tan⁡(θ)±tan⁡(φ)1∓tan⁡(θ)tan⁡(φ)\footnotesize\tan(\theta+\varphi) = \frac{\tan(\theta)\pm\tan(\varphi)}{1\mp\tan(\theta)\tan(\varphi)}

Of course, this identity simplifies for the double angle:

tan⁡(θ+θ)=tan⁡(2θ)=tan⁡(θ)±tan⁡(θ)1∓tan⁡(θ)tan⁡(θ)=2tan⁡(θ)1−tan⁡2(θ)\footnotesize\begin{split} \tan(\theta+\theta) &= \tan(2\theta)\\[.5em] &=\frac{\tan(\theta)\pm\tan(\theta)}{1\mp\tan(\theta)\tan(\theta)}\\[1em] & = \frac{2\tan(\theta)}{1-\tan^2(\theta)} \end{split}

Triple angle trig identities calculator

Triple angle identities follow the double angle identities closely, but they are both not as neat and not as expected: we can quickly see them. For the sine and the cosine, we see similar behavior:

sin⁡(3θ)=3sin⁡(θ)−4sin⁡3(θ)cos⁡(3θ)=4cos⁡3(θ)−3cos⁡(θ)\footnotesize \begin{split} \sin(3\theta) &= 3\sin(\theta)- 4\sin^3(\theta)\\[.5em] \cos(3\theta) &= 4\cos^3(\theta)-3\cos(\theta) \end{split}

As for the tangent, you can see that the formula is, once again, not as handy as the ones for the sine and cosine:

tan⁡(3θ)=3tan⁡(θ)−tan⁡3(θ)1−3tan⁡2(θ)\footnotesize\tan(3\theta) =\frac{3\tan(\theta)-\tan^3(\theta)}{1-3\tan^2(\theta)}

How to calculate half-angle identities

We left the half-angle identities last, but they are by no means less important. With these identities comes a catch: we need to specify the sign of the result, as all the expressions we use see square roots (which have ambiguous results). Here are the half-angle identities for sine and cosine:

sin⁡(θ2)=sgn(sin⁡(θ2))1−cos⁡(θ)2cos⁡(θ2)=sgn(cos⁡(θ2))1+cos⁡(θ)2\footnotesize \begin{split} \sin\left(\frac{\theta}{2}\right) &\!=\!\rm{sgn}\left(\!\sin\left(\frac{\theta}{2}\right)\!\!\right)\!\sqrt{\frac{1\!-\!\cos(\theta)}{2}}\\[1.5em] \cos\left(\frac{\theta}{2}\right) &\!=\!\rm{sgn}\left(\!\cos\left(\frac{\theta}{2}\right)\!\!\right)\!\sqrt{\frac{1\!+\!\cos(\theta)}{2}} \end{split}

Once again, the tangent disappoints us:

tan⁡(θ2)=1+sgn(cos⁡(θ))1+tan⁡2(θ)tan⁡(θ)\footnotesize\tan\left(\frac{\theta}{2}\right)\!=\!\frac{1\!+\!\rm{sgn}(\cos(\theta)\!)\sqrt{1\!+\!\tan^2(\theta)}}{\tan(\theta)}

🙋 To find out more about these identities, visit our half angle calculator!

How to use Omni's trig identities calculator

Omni's trig identities calculator is a collection of all the formulas and properties we listed above. You can find the values of other trigonometric functions, rotations, shifts, and so on, or even check the formulas if you are running out of memory.

Choose the desired type of identity you are considering in the first field on the top of the calculator, and let us do all the math. We will print the formulas and results for sine, cosine, and tangent.

FAQs

How do I calculate the cosine of a double angle?

To calculate the cosine of a double angle, follow these steps:

  1. Consider the trig identity for the cosine of the composite angle θ + φ:

    cos(θ + φ) = cos(θ)cos(φ) - sin(θ)sin(φ).

  2. Since we are working with a double angle, write: 2θ = θ + θ.

  3. Apply the composite angle identity to θ: θ + θ: cos(2θ) = cos(θ + θ) = cos(θ)cos(θ) - sin(θ)sin(θ) = cos²(θ) - sin²(θ).

The last identity is the double angle identity for the cosine.

What is the sine of 15°?

The sine of 15° is sin(15°) = 0.2588. To find this value, use the half-angle identity starting from the angle of 30°:

  1. The sine of the half-angle is:

    sin(α/2) = sgn(sin(α/2))√((1 - cos(α))/2)

    where sgn is the function that returns +1 or -1 depending on its argument.

  2. We know α = 15° is in the first quadrant; hence its sine is positive: sgn(sin(15°)) = 1.

  3. Substitute cos(30°) = √3/2 = 0.866 in the formula.

  4. Calculate √((1 - 0.866)/2) = √(0.067) = 0.2588.

What are the shift trig identities for the sine?

The trigonometric identities involving shifts of the argument of the sine are:

  • Shift by a quarter of the period (α → α ± 90°):

    sin(α ± 90°) = ±cos(α);

  • Shift by half of the period (α → α + 180°):

    sin(α + 180°) = -sin(α); and

  • Shift by full periods (α → α + 360°):

    sin(α + k · 360°) = sin(α) for any integer k.

What are trig identities?

Trig (trigonometric) identities are a set of equalities that compare single values of trigonometric functions to a composition of other trigonometric functions or to changes in the arguments. Trigonometric identities are a fundamental tool since there are no easy algorithms to calculate the values of sine, cosine, and tangent directly: careful compositions of reflections, shifts, rotations, etc. allow you to "build" the desired angle (or an approximation) and save you a lot of time!

Angle θ

Check out 21 similar trigonometry calculators 📐
ArccosArcsinArctan...18 more