Half Angle Calculator

Welcome to Omni's half-angle calculator, where we'll study half-angle trig identities. The double angle formulas let us easily find the functions of twice the angle. Here, we'd like to do the same, but instead of multiplying the angle by two, we'll divide it. In fact, the main tool to find the sin, cos, and tan half-angle formulas are the power reducing identities.

But let's not get ahead of ourselves! There's more than enough time in the upcoming sections to go through it all slowly and in detail.

We hope you're ready and fully awake because it's time to begin!

Triangles are the simplest geometric objects we can construct. They have three sides, three angles, and that's basically all there is to them. Arguably, we can't have a polygon that has two, not to mention one side. So since triangles are that easy, it should be quite simple to understand them, right?

In some sense, it is indeed the case. For example, there are quite a few ways to find the area of a triangle. Although not all of them are pretty (check out Heron's formula calculator, for instance), there are times when each can be useful.

Furthermore, as the simplest polygons, triangles have been studied thoroughly since ancient times (remember Pythagoras?). Well, he was not the first, nor the last to commit his life to them.) After all, we can divide every polygon into triangles (e.g., by drawing a few diagonals), so if we understand the basic object, we should be able to understand all the others.

Trigonometry might just be the most useful tool in triangle studies. The idea behind it is to relate the side lengths to the inside angles. After all, you can easily see that if you have a triangle and increase one of its angles, then the sides must change accordingly. It turns out that the "accordingly" can be translated into some really nice functions. Check the trigonometric functions calculator to learn more!

There is only one right way to start talking about trigonometric functions - the right triangles (pun fully intended). Angle-wise, they are the easy case: we know that one angle must be 90 degrees, so that leaves us with only two to worry about. We define the trigonometric functions by the formulas listed below:

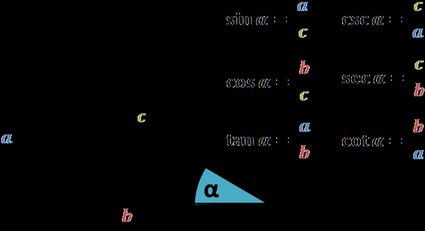
Note that we (and the half-angle identities calculator) limit ourselves to studying the sine, cosine, and tangent since the others are not as common in applications and textbooks.

There is, however, one significant drawback to the definitions above: the angle α must be between 0 and 90 degrees (or between 0 and π/2 radians) simply because it's a right triangle. Nevertheless, we can extend the definitions to any real value (even negative) by translating it all into a two-dimensional plane.

Let A = (x, y) be a point on the plane and denote by α the angle going counterclockwise from the positive half of the horizontal axis and the line segment connecting (0, 0) and A. (Observe how we said that α goes from one line to the other and not that it is between them. Because of that, we often call α a directed angle.)

Clearly, such an angle can be larger than 90 degrees. Even better - it can be larger than the full 360 degrees: it can make one full circle, and from 360 upwards begin its second lap. Also, since we've defined α to be directed, we can now have negative angles by simply going the other way, i.e., clockwise instead of counterclockwise.

For such angles, we extend the definitions of trigonometric functions from above by substituting in the formulas above a for y, b for x, and c for √(x² + y²) (the distance from (0, 0) to A).

Alright, we hope that we've managed to convince you that trigonometric functions are useful. It may take a week or two to befriend them, but that moment is sure to come. Before that happens, however, let's mention some nice identities that use them. Needless to say, we'll focus on the tan, sin, and cos half-angle formulas.

In trigonometry, once we become familiar with the functions, the next step is to study the relations between them. It turns out that not only does, say, sine describe the ratio of a triangle's sides, but it is also connected to the cosine by nice and useful formulas.

The study of trigonometric identities and equations could easily fill a whole book or two. As a small encouragement to delve into the topic, let's mention two that appear quite often when dealing with triangles: the law of sines and the law of cosines.

We, however, have gathered here today to study the half-angle identities. And to understand where they come from, we'll use the so-called power reducing formulas. Below, we list the identities, but if you'd like to learn more about them, be sure to check out Omni's dedicated power reducing calculator.

A keen eye will observe that in each formula on the right, we have twice the angle that we have on the left. To be precise, the one on the left is half of the one on the right. And that's precisely what we need!

Firstly, take the top formula. We rewrite it with an angle of $\frac{x}{2}$ on the left and with $x$ on the right (note that this notation must only keep the relation that one is half of the other) and take the square root of both sides.

Observe that we need the $\pm$ sign because of the properties of an even exponent. In practical calculations, the sign depends on which quadrant of the plane we are in with our angle.

The cos half-angle formula is obtained similarly:

Lastly, we take the tangent power reducing identity and do the same to get the tan half-angle formula. Note that equivalently, we could use the trigonometric identity $\tan\left(x\right) = \frac{\sin\left(x\right)}{\cos\left(x\right)}$.

Additionally, we can get two other tan half-angle formulas (which are also listed in the half-angle formula calculator) that have the advantage of not having the $\pm$ sign. They come from using the double angle identities together with the $\tan\left(x\right) = \frac{\sin\left(x\right)}{\cos\left(x\right)}$ formula and the Pythagorean identity of $\sin^2\left(x\right) + \cos^2\left(x\right) = 1$. Indeed, on the one hand, we have

and on the other hand, similarly,

Aaand with that, we declare the end of theory for this article. After all this time spent reading through formulas, it's time for some numeric examples, and that's what the next section is all about!

Finally, your biggest dream has come true - you bought yourself a little hut in the mountains! Well, it's not really a hut just yet, so far it's only a piece of land that you'll be building on, but it's most certainly a start. And after consulting our time value of money calculator, you've decided that it's the best form of investment.

You've taken social distancing to the next level and chosen an area far away from civilization. Unfortunately, this means that even before you let in a crew to put down some concrete foundations, you have to make sure that the machinery can get there safely. In particular, you need to prepare a stable driveway, at least a gravel one. There will come a time to upgrade it to asphalt, but for now, it will have to do.

There is one place that requires some extra attention - a 30-degree slope that is a serious obstacle for heavier construction equipment. However, the crew tells you that if only you could flatten it out to half that, then it should be fine.

Wait, did anyone mention halving an angle? Now, this should be a piece of cake for the half-angle calculator!

For precise data of what, where, and how you should flatten, you need to do some calculations about the slope. For that reason you can head to our slope calculator where we explained it in detail. To find gradient of a slope, it'd be useful to know the trigonometric functions of the angle you're dealing with. (After all, we can think of the slope as the hypotenuse of a large right triangle.) Of course, we could just Google the data, but where's the fun in that? Answer: the fun is in using the half-angle identities calculator!

Let's break it down into a simple step-by-step solution/instruction.

• We know that the slope is at a 30-degree angle, and we'd like to reduce it to half that. To find the trigonometric functions in this case, it is enough to enter into the half-angle calculator the data that we begin with.
• Under "Angle" we input the 30 degrees, and the moment we do, the tool will spit out the answer, both for the full angle and the halved one.
• Note also that 30 is a special case of a right triangle, so the half-angle calculator will show you the precise values of the trigonometric functions before we round them up, i.e., in the form of a fraction with square roots.

Just on the side, let us now see how to use the half-angle trig identities to find the answer by hand. So grab a piece of paper, and let's get to it!

First of all, let's begin with the obvious: half of 30 degrees is 15 degrees. This means that our half-angle is in the first quadrant (because it's between 0 and 90 degrees). This further translates to the sine, cosine, and tangent being positive. Therefore, for the sin, cos, and tan half-angle formulas, we'll use the identities with a $+$ where we had the $\pm$ sign.

We'll begin with sine. Recall that $\cos\left(30 \degree\right) = \frac{\sqrt{3}}{2}$, so:

Next, the cos half-angle formula gives:

Lastly, from the tan half-angle formula, we obtain:

And there it is! We now have all the information needed to get to work and reduce that angle of ascension. Or... Maybe first, a short hike up the mountain? The job can wait an hour or two, can't it?

To calculate the sine of a half angle sin(x/2), follow these short steps:

1. Write down the angle x and replace it within the sine of half angle formula:

   sin(x/2) = ± √[(1 - cos x)/2].

2. Determine the sign using the half angle:

   • Positive (+) if the half angle lies on the 1st or 2nd quadrants; or
   • Negative (-) if it lies on the 3rd or 4th quadrants.

√[(2 + √3) / 2]. Since 15° is half of 30°, you can use the half-angle formula for cosine to find the cosine of 15°:

cos(30°/2) = ±√[(1 + cos 30°)/2] = √[(2 + √3) / 2].

The sign of trigonometric identities involving half-angles depends on the quadrant where the half-angle is and the trigonometric function:

• Sine:
  • Positive if half angle lies on 1st or 2nd quadrants. Negative otherwise.
• Cosine:
  • Positive if half angle lies on 1st or 4th quadrants. Negative otherwise.
• Tangent:
  • Positive if half angle lies on 1st or 3rd quadrants. Negative otherwise.

No. The expression cos(x/2) refers to the cosine of half an angle x, while cos(x)/2 is half the cosine of x. To modify the argument of a trigonometric expression, you need to use trigonometric identities, such as the cosine of half an angle:

cos(x/2) = ±√[(1 + cos 30°)/2].