Power Reducing Calculator

Welcome to Omni's power reducing calculator, where we'll study the formulas of the power reducing identities that connect the squares of the trigonometric function (sin²(x), cos²(x), and tan²(x)) to the cosine of the angle doubled (i.e., using the cos(2x) identity). It is a quick and easy way to go between different powers of trigonometric functions, either from smaller to larger or vice versa.

So sit back, grab a cup of coffee, and let's get to it!

Geometrically speaking, the world is made of triangles. The best proof of this is in video games: all graphics, especially those in three dimensions, are done by combining a lot of triangles to form a pattern that resembles a person, animal, or object. Starting from a square, you can just slice it in two along the diagonal to get two triangles. The more complex the object, the more triangles it needs. But in the end, it's just more of the same three-edged shape. Even circles can be approximated by a sufficient number of triangles.

In fact, this is a good thing because triangles are easy to work with. They only have three sides, and, what is more, once we know their lengths, we also know their angles. The opposite is also true, but we can't know the size of the triangle. You can verify those two facts with our triangle angle calculator.

The above is a very non-trivial fact. What it says is that, basically, no weird things can happen. The correspondence between the angles and the sides must satisfy several properties. This is precisely the motivation behind trigonometry and trigonometric functions. It greatly simplifies triangle studies since, instead of worrying about measuring three sides and three angles, we can work only with the functions.

The introduction to trigonometric functions is usually done on right triangles. Below you can find the formulas for almost all the trigonometric functions. Let us mention here that, in reality, we mostly limit ourselves to the sine (sin), cosine (cos), and tangent (tan) functions (learn more about them in our trigonometric functions calculator)

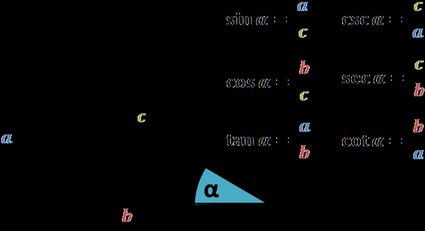
Note that, as the name suggests, these are functions, so they associate a number to an argument, the latter being an angle. Also, since we're dealing with right triangles, the argument cannot be larger than 90° (or π/2 in radians).

However, we can extend all the trigonometric functions to any angle, even a negative one. To do that, we look at the two-dimensional Euclidean space. For a given point A = (x, y) in that space, denote by α the angle between the positive half of the horizontal axis to the interval from (0,0) to A going counterclockwise. Clearly, this angle can be larger than 90°.

Now, we translate all the trigonometric function formulas from above to this new setting by exchanging b for x, a for y, and c for the distance from A to (0,0) (which is equal to √(x² + y²).

We've already mentioned that trigonometric functions describe the correspondence between the sides and the angles of a triangle. What we'd like to do next is find some correspondences between the correspondences or, if you prefer, formulas using the above functions. We call such equations trigonometric identities, and we can't stress enough how important they are.

As seen in the law of sines calculator and the law of cosines calculator, trigonometric identities can sometimes provide us with additional info about the triangle. Other times, they simplify longer, tedious trigonometric calculations. The power-reducing identities are an example of the latter.

Before we see the power-reducing formulas themselves, let's introduce two other trigonometric properties, which will, in fact, imply the power-reducing identities.

The (fundamental) Pythagorean trigonometric identity states that

sin²(x) + cos²(x) = 1

for any angle x. If you're not convinced that such a pretty formula is true, we encourage you to take a minute to prove it. It's enough to substitute for sin(x) and cos(x) the quotients from the section above and use the Pythagorean theorem.

Next, we'll need the cos(2x) identity. It states that:

cos(2x) = cos²(x) - sin²(x)

for any angle x.

Now, if we use the first formula to rewrite the second, on the one hand, we'll get

cos(2x) = cos²(x) - sin²(x) =

cos²(x) - sin²(x) + 1 - 1 =

cos²(x) - sin²(x) + 1 - cos²(x) - sin²(x) =

-2sin²(x) + 1,

and on the other hand,

cos(2x) = cos²(x) - sin²(x) =

cos²(x) - sin²(x) + 1 - 1 =

cos²(x) - sin²(x) + cos²(x) + sin²(x) - 1 =

2cos²(x) - 1.

Next, in the first one, we move the 1 to the left and divide both sides by -2. This way, we obtain:

cos(2x) = -2sin²(x) + 1

(cos(2x) - 1) / (-2) = sin²(x)

sin²(x) = (1 - cos(2x)) / 2.

Similarly, the second formula gives

cos(2x) = 2cos²(x) - 1

(cos(2x) + 1) / 2 = cos²(x)

cos²(x) = (1 + cos(2x)) / 2.

These are our first two power-reducing identities. To find the last one, that with tangent, recall one more basic trigonometric formula:

tan(x) = sin(x) / cos(x)

for x not equal to 90° + k×180° (or π/2 + kπ in radians), where k is any integer. This allows us to find the third power reducing formula by simply applying the two we got above:

tan²(x) = (sin(x) / cos(x))² = sin²(x) / cos²(x) =

= [(1 - cos(2x)) / 2] / [(1 + cos(2x)) / 2] =

= (1 - cos(2x)) / (1 + cos(2x)).

Now, those don't seem too bad, do they? Certainly, the proofs didn't take too long. Just to be on the safe side, let's conclude the section by listing the three of them in a nice, concise way:

And with that, we conclude the theoretical part of the article. It was fun, wasn't it? Still, how much time can you spend looking at symbols instead of the good ol' numbers? Well, next up is a section to address just that and show you the possibilities of the power-reducing calculator!

Suppose that you have a test in trigonometric functions coming later this week. From what the teacher says, it will focus on calculating the values of the functions at specific angles and using some trigonometric identities (including the power-reducing formulas) to help you along the way.

You decide to grab the exercise book and go through at least a few examples to prepare yourself. The first one tells you to calculate:

sin²(x) - sin⁴(x)

for x = 15° (or x = π/12 in radians).

Now, this looks like a job for the power-reducing calculator!

First of all, let's see how easy it is to find the answer using our tool. For that, we'll divide the task into three parts:

1. Finding sin²(x);
2. Finding sin⁴(x); and
3. Calculating the difference.

Take a look at the power-reducing calculator. At the top, we have a field with the variable "angle". This is the x in the formulas, as you can hopefully see above the calculator. Oh, just like in the exercise! What a coincidence!

We input the number:

x = 15°.

The moment we do that, the power-reducing calculator spits out the answer for sin²(x) (and other functions, which we don't need at the moment). Yay, we have the first part!

Now how do we find sin⁴(x)? Well, it's crucial to observe that

(sin²(x))² = sin⁴(x).

This means that we can either just take the square of sin²(x) that we got above or... use the power-reducing calculator again!

The best thing about Omni calculators is that they work in multiple ways. This means that instead of inputting the angle, we can now input the value of the sine, and that's precisely what we'll do here. If we write the value of sin²(x) under sin(x) in the power-reducing calculator, then the tool will spit out the value of sin⁴(x) (i.e., the square of what we input) in the sin²(x) window.

Magical, isn't it? Note, however, that the calculator will also show the angle that the value corresponds to, which is different from the 15° from the exercise.

And once we have the two values, we can subtract them and get the answer to our problem. However, let's not spoil it for ourselves just yet! It's time to grab a piece of paper and calculate the whole thing ourselves.

First of all, note that 15° is a weird angle in the sense that it's not so clear what its trigonometric functions are. Fortunately, however, we don't need it! "How so?" you may ask. Well, let's see.

We need to find sin²(x) and sin⁴(x). But we've learned a thing or two about sin²(x) in the above section, didn't we? That's right – in the power-reducing identities!

According to the power reducing formula for the sine, we have:

sin²(x) = (1 - cos(2x)) / 2.

In our case, this translates to:

sin²(15°) = (1 - cos(2 × 15°)) / 2 = (1 - cos(30°)) / 2.

Wait, doesn't it look familiar – the cosine of 30°? Sure it does; it's the function corresponding to a right triangle with angles 90°, 60°, and 30°, explained in the 30 60 90 triangle calculator. There's no need for the cos(2x) identity or anything.

Moreover, we know its sides quite well, or rather the ratios between them. If we recall the formula of the cosine, this tells us that:

cos(30°) = √3 / 2 ≈ 0.865.

We substitute it into the power reducing formula:

sin²(15°) = (1 - cos(30°)) / 2 ≈ (1 - 0.865) / 2 ≈ 0.068.

Lastly, we use a similar trick as before to find sin⁴(15°):

sin⁴(15°) = (sin²(15°))² ≈ 0.068² ≈ 0.005,

which tells us that the final answer is:

sin²(15°) - sin⁴(15°) ≈ 0.068 - 0.005 = 0.063.

Great, we've finished the exercise! If anything like that appears on the test, we'll be more than ready!