Partial Fraction Decomposition Calculator

Welcome to Omni's partial fraction decomposition calculator, where we'll take a rational expression and write it as several simpler ones. The process can prove very useful, for instance, when computing integrals: the initial function may be tricky to deal with, but the individual summands; not so much. We'll learn all the partial fraction decomposition rules (there aren't many, don't worry) and see how to do partial fraction decomposition on a nice example.

So without further ado, let's see what this partial fraction expansion is all about!

Polynomials are algebraic expressions that contain variables only in non-negative integer powers. In other words, they describe functions that consist of numbers, letters (i.e., variables), and basic arithmetic expressions. However, the variables cannot appear under a root, inside functions (e.g., trigonometric functions or logarithms), with fractional powers, etc.

A few examples of polynomials are:

• $x + 2y$;

• $a^2 + 2ab + b$;

• $n^3 - 0.7n + \frac{3}{8}$; and

• $1 + 3 + x^5 - x^7 + 19x^9$.

Note how there may be more than one letter in a polynomial. Nevertheless, today we'll focus only on those with a single one, just like the partial fraction decomposition calculator.

In mathematics, a quotient of two polynomials is often called a rational function or a rational expression. Needless to say, such objects are a bit more difficult to operate than simple polynomials. Just look at an example of such a monstrosity:

Luckily, there are ways to write such things in a nicer way. A sum of several rational expressions, true. But prettier ones!

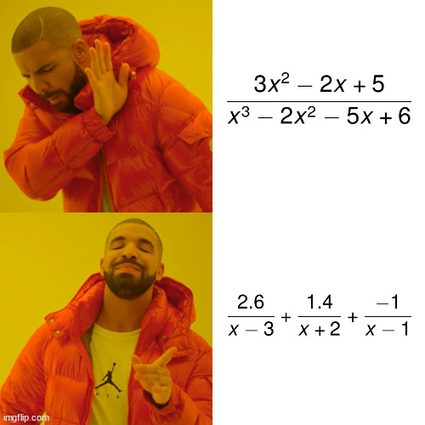
However, before we see how to do partial fraction decomposition, we need to go through several math properties. The very basic one concerns factoring polynomials.

When we work with real numbers (anything from $1$, through fractions, roots, up to numbers such as $\pi$ and the Euler number $\mathrm e$), every polynomial can be decomposed into factors of degree $1$ or $2$. In other words, however large the exponents of your polynomial, you can write the whole thing as a product of binomials and quadratic polynomials. For instance,

In fact, the quadratic factors appear (i.e., cannot be decomposed into two of order $1$) only when they have no real roots. If we were to move to complex numbers, we would obtain only binomials in the expansion. Either way, these factors are what appears in the denominators of the partial fraction formula.

In general, factoring polynomials of a high order is an extremely difficult problem. Feel free to check out Omni's algebra calculators section to find some useful tools to help with that, such as synthetic division calculator or the rational zeros calculator.

We've already mentioned what appears in the partial fraction formula, but we've yet to see it in detail. It's now time to study it in depth, together with the partial fraction decomposition rules that govern the whole thing.

In the above section, we've introduced factoring polynomials. However, it's important to remember that each factor can appear multiple times. For instance,

In general, let's say we want to find the partial fraction expansion of the quotient $P(x) / Q(x)$ of two polynomials, where $P(x)$ is of a smaller degree than $Q(x)$ (if it weren't, we first need to pull the higher exponents out of the quotient; for details see the next section). Assume that $Q(x)$ factorizes as:

Then the partial fraction decomposition rules for $P(x) / Q(x)$ are as follows:

• The partial fraction expansion has $k_1 + k_2 + ... + k_n$ summands.

• The denominators of the quotients take the form $(W_i(x))^t$ with $t$ ranging from $1$ to $k_i$. In other words, we have one quotient with $W_i(x)$, one with $(W_i(x))^2$, one with $(W_i(x))^3$, and so on up to $(W_i(x))^{k_i}$.

• The numerator of the summand with $(W_i(x))^t$ in the denominator is of degree one smaller than $W_i(x)$. To be precise, it can be either of degree $0$ if $W_i(x)$ is linear or of degree $1$ if $W_i(x)$ is quadratic.

All in all, the partial fraction formula we end up with looks like this:

where the polynomials $A_{i,j}(x)$ are one degree smaller than $W_i(x)$.

Fair enough, the partial fraction formula does look scary when you see it in full generality. However, in applications, it all boils down to fairly simple calculations. Note how Omni's partial fraction decomposition calculator admits only polynomials of degree up to $3$, which is already a considerable simplification. After all, it means that there may be at most three factors when rewriting $Q(x)$, which further gives at most three summands in the partial fraction expansion.

Still, there's one more thing that this formula doesn't give: how to do partial fraction decomposition in practice? In particular, how do we find the polynomials $A_{i,j}(x)$?

Well, let's find out, shall we?

Let's begin with clear step-by-step instructions of what we need to do with a quotient $P(x) / Q(x)$ to find its partial fraction expansion before we go into details.

1. If the degree of $P(x)$ is greater or equal to that of $Q(x)$, pull its higher exponents out of the quotient.
2. Decompose $Q(x)$ into irreducible factors of degree $1$ or $2$.
3. (Optional) Compare the factors with $P(x)$ to see if you can reduce anything.
4. Use the partial fraction formula from the above section to write what the expansion should look like. For now, use $A_{i,j}(x)$ as unknown.
5. Solve the equation to find the polynomials $A_{i,j}(x)$. To do so, you need to:
   • Write the polynomials $A_{i,j}(x)$ in the form $Ax + B$ or simply $A$, depending on their degree (for now, $A$ and $B$ are unknown numbers),
   • Multiply both sides by the denominator of the left side,
   • Simplify both sides;
   • On the right side, group summands that correspond to the constant factor, to $x$, to $x^2$, and so on;
   • Write and solve the system of equations coming from comparing the coefficients of different powers of $x$ on both sides to find the $A\mathrm{'s}$ and $B\mathrm{'s}$ (check the system of equations calculator if you need help); and
   • Substitute what you've found in the initial partial fraction formula.
6. Celebrate with a piece of cake. You deserve it!

We'll go through it all on a nice example in the next section, but for now, let's briefly comment on the list above.

Ad.1) If the degree of $P(x)$ is greater or equal to that of $Q(x)$, it is always possible to find $D(x)$ and $R(x)$ such that:

with $R(x)$ of degree smaller than that of $Q(x)$. In essence, $D(x)$ is the result of polynomial division of $P(x)$ by $Q(x)$, and $R(x)$ is the non-divisible rest obtained through the process.

Ad.2) For more information on that, see the first section.

Ad.3) The simpler the expression, the easier the further calculations. For instance, why bother with $(2x^2 + 4x + 2) / (2x^3 + x^2 - 4x - 3)$ if it's the same as $2 / (2x - 3)$? Nevertheless, the partial fraction expansion we get will be the same in both cases: some summands in the first case will simply get numerators equal to zero.

Ad.4) Before you use the partial fraction decomposition formula, make sure there's a point to do so. After all, if your expression itself already looks like a summand from the formula (for instance, $2 / (2x - 3)$ we've mentioned above), then you won't get anything better than that.

Ad.5) Arguably, the hardest point on the list. At consecutive bullet points, remember about:

• Different notation for each numerator;
• The rules for polynomial multiplication;
• The rules for adding and subtracting polynomials;
• Taking into account all summands with the same power of $x$ (in general, every variable from the first bullet point can contribute to a given $x^k$);
• The above bullet point describes the coefficients corresponding to $x$, $x^2$, and so on in terms of the variables from the first bullet point – these are precisely the equations of your system; and
• Making sure you don't mix up the variables when substituting them.

Ad.6) What, you don't think you deserve any cake? Oh, come on! There'll be time for perfecting your beach body after we perfect your algebra skills.

Alright, now that we have a clear list of what to do, it's time to keep our promise – show how to do partial fraction decomposition on a nice example.

Let's see how to do partial fraction decomposition on the following example quotient:

However, before we sit down to compute the solution ourselves, let's see how easy the task is when we use the partial fraction decomposition calculator.

In our tool, we see the variable fields divided into two sections: one dedicated to the numerator and one to the denominator. We begin by choosing the degree of the polynomials: in our case, it's $3$ for both, so we choose that option from the lists. Note how the partial fraction decomposition calculator then lets you choose the form in which you input the polynomials while showing the notation the tool uses at the same time.

Looking back at our quotient, we see that the expressions are in their basic forms, i.e., are not decomposed into factors, so we choose $a_3x^3 + a_2x^2 + a_1x + a_0$ for the numerator and $b_3x^3 + b_2x^2 + b_1x + b_0$ for the denominator. Below each, we see fields where we input the variables' values. In our case, they are:

• $a_3 = 2$, $a_2 = 1$, $a_1 = -4$, $a_0 = 1$,

• $b_3 = 1$, $b_2 = -2$, $b_1 = -2$, $b_0 = -3$.

Once we give the last number, the partial fraction decomposition calculator spits out the answer underneath together with the intermediate steps.

Simple, wasn't it? Well, let's now see how much time the tool saved us and try to find the partial fraction expansion ourselves. We will follow the instructions from the above section.

First of all, note how the degree of the numerator is the same as that of the denominator. To fix that, we can try dividing the two polynomials, or, alternatively, tilt our heads to the side, bite our lips in focus, and observe that:

which means that:

All in all, it's $(5x^2 + 7) / (x^3 - 2x^2 - 2x - 3)$ that we have to worry about.

Next, we need to decompose the denominator into factors. Again, we can cleverly note that:

What is more, quadratic formula calculator tells us that the second factor above has no roots, so this decomposition is as good as we can get. According to the partial decomposition formula from the second section, this tells us that the expansion will look like this:

However, we need to remember that $A_{1,1}(x)$ and $A_{2,1}(x)$ are of degrees $0$ and $1$, respectively (because the denominators are of degrees $1$ and $2$, respectively). Therefore, we can write $A_{1,1}(x) = A$ and $A_{2,1}(x) = Bx + C$ with $A$, $B$, and $C$ some real numbers that we'll try to find now.

Now, we follow the instructions from the above section to find a system of equations that will lead us to the answer.

We compare the coefficients at $x^2$, at $x$, and at the constant term to obtain the following three equations:

• $A + B = 5$,

• $A - 3B + C = 0$,

• $A - 3C = 7$.

Since we focus here on partial fraction decomposition, we'll skip solving the system. Feel free to use your favorite method, be it Cramer's rule, or use the elimination method calculator. Either way, you should arrive at the following solution:

• $A = 4$, $B = 1$, $C = -1$.

Lastly, we substitute these numbers into the formula above to obtain:

Phew, that may not have been super difficult, but it sure took some time. It's a good thing we have Omni's partial fraction decomposition calculator at hand, wouldn't you say?