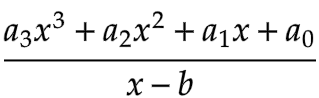Synthetic Division Calculator

Welcome to our synthetic division calculator! It helps you perform the synthetic division of polynomials while showing all the intermediate steps at the same time!

Have you ever wondered what synthetic division is? Do you need to learn how to do synthetic division? We teach you everything you need to know about dividing polynomials using synthetic division, provide examples of synthetic division with steps, and explain how to use synthetic division to find zeros.

As a bonus, we show you how to deal with non-monic and quadratic divisors!

Before we can explain how to divide polynomials using synthetic division, let's refresh a few basic notions:

What are polynomials?

A polynomial is an expression involving a sum of non-negative integer powers of at least one variable, each multiplied by real (or complex) numbers, which we call coefficients.

A polynomial in one variable, x (a univariate polynomial), is given by

a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀,

where a_n, a_n-1,..., a₁, a₀ are the coefficients. We call the individual terms of the form a_kx^k monomials. The leading coefficient of this polynomial is the coefficient of the term with the highest power of x, i.e., the coefficient a_n, provided that a_n ≠ 0. We say a polynomial is monic if its leading coefficient is equal to one: a_n = 1.

The degree of a polynomial is the value of the greatest exponent present in the polynomial with a non-zero coefficient. The polynomial written above has degree n, provided that a_n ≠ 0. Constant non-null polynomials have degree zero. A null polynomial has its degree left undefined or, sometimes, defined as -∞ (negative infinity). We usually denote the degree of a polynomial with deg.

Polynomial division

The division of polynomials is analogous to dividing integers with remainder, which you've most probably encountered in arithmetic. Let P(x) and D(x) be two polynomials. If D(x) is non-zero, then there exist two polynomials, Q(x) and R(x), which satisfy:

P(x) = D(x) ⋅ Q(x) + R(x)

and deg(R) < deg(D). Moreover, Q(x) and R(x) are unique, i.e., there's no other pair of polynomials that satisfy these two conditions.

The terms we use in polynomial division are analogous to those in arithmetic: P(x) is called the dividend, D(x) is the divisor, Q(x) is a quotient, and R(x) is the remainder.

Note that:

• R(x) = 0 if, and only if, P(x) has D(x) as a factor; and
• If deg(P) < deg(Q), then D(x) = 0 and P(x) = R(x).

The standard way of calculating the quotient and remainder, given a dividend and divisor, is via the algorithm called the polynomial long division.

What is the synthetic division of polynomials?

Synthetic division is a shortcut way of dividing polynomials. It gives the same results as the polynomial long division but is much faster as it involves only the coefficients of the dividend and divisor, on which we perform basic arithmetic operations. As a result, we obtain the coefficients of the quotient and the remainder.

At a first look, you may find synthetic division a bit complicated, but rest assured: once you get the hang of it, you'll never look back!

Synthetic division is most commonly used when dividing by linear monic polynomials x - b. Dividing by such polynomials is very important in the context of finding zeroes and factoring polynomials: to verify whether b is a root of a polynomial, we can synthetically divide this polynomial by x - b and check if the remainder is equal to zero. For details, check out the section below, where we discuss how to use synthetic division to find the zeros of a polynomial.

Keep in mind that synthetic division works for any polynomial divisors: for non-monic polynomials as well as for polynomials of degrees higher than one. However, it becomes more and more complicated as the degree of the divisor grows. In this article, we'll discuss in detail some synthetic division examples of non-monic linear polynomials b₁x + b₀ and quadratic polynomials c₂x² + c₁x + c₀.

So, let's dive in and learn how to divide polynomials using synthetic division!

This section describes how to do synthetic division if the divisor is of the form x - b. For examples of synthetic division with divisors of a more complicated form, see the subsequent sections.

Since synthetic division is best explained with an example, we'll divide 3x³ - 8x - 9 by x - 2. Let's discuss in detail how to do synthetic division.

1. Set up the synthetic division table. It consists of three rows:

   • In the first row, put the coefficients of the dividend in descending powers of x, inserting 0's for any missing powers. In our example, the x² term is missing, so we add 0 between 3 and -8, i.e., between the coefficients of x³ and x.

   • In the second row and one column to the left, write b from the divisor x - b. In our case, b = 2. It is common to write the multiplication sign in front of b and to separate it from the coefficients with a vertical bar. This is because the role this number plays in synthetic division is different than that of the coefficients.

   • We leave the third row blank - we'll fill it up as we go.

2. Drop the leading coefficient of the dividend to the bottom row.

3. Multiply this dropped number by the number b on the left (in our case, it's multiplication by 2). Place the result under the next coefficient of the dividend.

4. Sum the numbers in the column we created in the previous step. Write the result in the bottom row.

5. Repeat Steps 3. and 4. until the table is full. We'll show you how to do it:

• Multiply the 6 we obtained above by b = 2 and write the result in the next column.

• Add -8 and 12 together and write the sum in the last row.

• Multiply the 4 we obtained above by b = 2 and write the result in the next column.

• Add -9 and 8 together and place the result in the last row.

6. OK, the table is full. The result of the polynomial division we're looking for is here: the coefficients of the quotient and the remainder of this division can be found in the last row of our table!

The last value on the right is the remainder, and all the other values are the consecutive coefficients of the quotient, starting from the leading coefficient (working left to right):

• Coefficients of the quotient: 3, 6, 4
• Quotient: 3x² + 6x + 4
• Remainder: -1

We will now see how to perform a synthetic division if the divisor is in the form b₁x + b₀, i.e., linear but not necessarily monic. As an example, let's divide 4x³ + 2x² - 2x + 1 by 2x + 1.

1. Set up the division table. It's very similar to that for monic divisors, but the main difference is the presence of the fourth row, where we place the leading coefficient b₁ of the divisor preceded by the division sign :. Also, be careful with the signs: we write -b₀ at the beginning of the second row!

2. Drop the leading coefficient of the dividend to the third row.

3. Divide the number you've just placed in the third row by 2 and put the result in the last row.

4. Multiply this dropped number by the number on the left. Place the result under the next coefficient of the dividend.

5. Sum the numbers in the column we created in the previous step. Write the result in the third row.

6. Repeat Steps 3. & 4. & 5. until the table is (almost) full – you don't need to perform the last division.

   In our example, we obtain the following table (check it yourself!):

7. This time, to find the coefficients of the quotient and the remainder, you need to take a look at the last two rows of our table.

The last value of the penultimate row is the remainder of the division, and the values in the last row are the coefficients of the quotient: working left to right, the first number is the leading coefficient of the quotient, and the last one is the constant.

• Coefficients of the quotient: 2, 0, -1
• Quotient: 2x² - 1
• Remainder: 2

We will now see how to perform a synthetic division if the divisor is a quadratic polynomial of the form c₂x² + c₁x + c₀. As an example, let's divide 6x⁴ + 7x² - 3 by 2x² - 4x + 5.

1. Set up the division table. Similarly to the non-monic linear case, the leading coefficient of the divisor, c₂ (preceded by the division sign /), is placed in the last row. However, we need two rows for two non-leading coefficients of the divisor: we put -c₀ in the second row, and -c₁ in the third row and to the left so that these two numbers form a downward left diagonal. And, as always, be careful with the signs!

2. Drop the leading coefficient of the dividend to the penultimate row.

3. Divide the number you've dropped by 2 and put the result into the last row.

4. Multiply the result from the previous step by the numbers before the bar and place the results diagonally: the result of multiplying by 4 goes under the second coefficient, and the result of multiplying by -5 goes under the third coefficient.

5. Sum the numbers in the column we created in the second column and put the result into the penultimate row.

6. Repeat Steps 3. & 4. & 5. until the penultimate row is full, i.e.:

• Divide 12 from the previous step by 2 and put the result into the last row.

• Multiply 6 by the numbers before the bar and place the results diagonally. The result of multiplying by 4 goes under the third coefficient, and the result of multiplying by -5 goes under the fourth coefficient.

• Sum the numbers in the third column and put the result in the penultimate row.

• Divide 16 by 2 and put the result into the last row.

• Multiply 8 by the numbers before the bar and write the results diagonally. The result of multiplying by 4 goes under the fourth coefficient, and the result of multiplying by -5 goes under the fifth coefficient.

• Sum the numbers in the fourth and fifth columns and put the results into the penultimate row.

7. Again, the quotient's coefficients and the remainder of the division wait for us in the last two rows of our table.

The two last values of the penultimate row are the coefficients of the remainder, and the values in the last row are the coefficients of the quotient. In both cases, working left to right, the first number is the leading coefficient of the quotient, and the last one is the constant.

• Coefficients of the quotient: 3, 6, 8
• Quotient: 3x² + 6x + 8
• Coefficients of the reminder: 2, -43
• Reminder: 2x - 43

We often use synthetic division to verify if a potential polynomial zero is an actual zero. Let p be a polynomial. If b is a candidate for a root of p, we synthetically divide p by x - b and look at the remainder. It follows that:

• If the remainder is zero, then b is a root of p; and
• If the remainder is non-zero, b is not a root of p.

This method is sometimes called factor theorem and it is a particular case of the polynomial remainder theorem (also known as the little Bézout's theorem), which states that the value of p at an argument b is equal to the remainder of the polynomial division p(x) / (x - b). In particular, x - b divides p(x) with null remainder if, and only if, b is a root of p.

Hence, to determine p(b), you need to perform the synthetic division of p by x - b, and the remainder gives you the value of p(b). The quotient can be used to factor p, as we explain below.

Why would you want to determine p(b) via the synthetic division method and not by naive evaluation, that is, by substituting x with b and evaluating this expression? It turns out that synthetic division is much more effective because we need to do fewer multiplications.

How to factor a polynomial using synthetic division?

Assume we have an integer-coefficient polynomial of degree n with n rational roots (counting with multiplicities). To factor such a polynomial with the help of synthetic division, follow these steps:

1. List all the potential rational roots of your polynomial using the rational root theorem. See the rational zeros calculator if you need help.

2. Test a candidate b for a root by looking at the remainder obtained in the synthetic division of our polynomial by x - b, as we explained above.

3. Once you have found an actual root, factor it out from the original polynomial. Determine the quotient from the synthetic division table.

4. Test the next candidate for a root, taking the quotient obtained above as the dividend.

5. Repeat Steps 3. and 4., i.e., keep testing potential roots using the subsequent quotients until you factor the original polynomial into linear factors.

Once you know what synthetic division is, you may want to experiment a bit with this technique of dividing polynomials. There's no better tool than our synthetic division calculator! Here we briefly explain how you can use it to divide polynomials like a pro:

1. Start by choosing the degree of the dividend. The highest available degree is 6.

2. Tell us the form of the divisor: you can choose between a linear or quadratic polynomial. There's also a monic linear polynomial of the form x - b, which you should choose if you use synthetic division to find the dividend's zeros. In such a case, b is a potential zero you want to test.

3. Enter the coefficients of the dividend and the divisor.

4. Our synthetic division calculator returns the synthetic division table along with the division result: the quotient and remainder.

5. Do you want to understand how to do synthetic division step-by-step? No problem! Our synthetic division calculator can display the synthetic division steps! You just need to set the Show steps option to Yes.