Triangle Angle Calculator

Triangle angle calculator is a safe bet if you want to know how to find the angle of a triangle. Whether you have three sides of a triangle given, two sides and an angle or just two angles, this tool is a solution to your geometry problems. Below you'll also find the explanation of fundamental laws concerning triangle angles: triangle angle sum theorem, triangle exterior angle theorem, and angle bisector theorem. Read on to understand how the calculator works, and give it a go - finding missing angles in triangles has never been easier!

There are several ways to find the angles in a triangle, depending on what is given:

1. Given three triangle sides

Use the formulas transformed from the law of cosines:

So:

For the second angle we have:

So:

And eventually, for the third angle:

So:

2. Given two triangle sides and one angle

If the angle is between the given sides, you can directly use the law of cosines to find the unknown third side, and then use the formulas above to find the missing angles, e.g. given a,b,γ:

• calculate $c = \sqrt{a^2 + b^2 - 2ab \times \cos(\gamma)}$;
• substitute $c$ in $\alpha = \mathrm{arccos}\left((b^2 + c^2- a^2)/(2bc)\right)$;
• then find $\beta$ from triangle angle sum theorem: $\beta = 180\degree- \alpha - \gamma$

If the angle isn't between the given sides, you can use the law of sines. For example, assume that we know $a$, $b$, and $\alpha$:

So:

• As you know, the sum of angles in a triangle is equal to $180\degree$. From this theorem we can find the missing angle: $\gamma = 180\degree- \alpha - \beta$.

3. Given two angles

That's the easiest option. Simply use the triangle angle sum theorem to find the missing angle:

• $\alpha = 180\degree- \beta - \gamma$;
• $\beta= 180\degree- \alpha - \gamma$; and
• $\gamma = 180\degree- \alpha- \beta$

In all three cases, you can use our triangle angle calculator - you won't be disappointed.

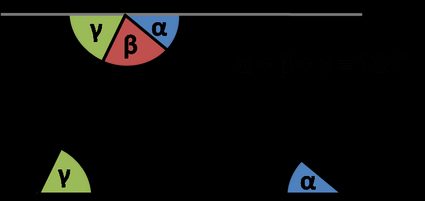
The theorem states that interior angles of a triangle add to $180\degree$:

How do we know that? Look at the picture: the angles denoted with the same Greek letters are congruent because they are alternate interior angles. Sum of three angles $\alpha$ $\beta$, $\gamma$ is equal to $180\degree$, as they form a straight line. But hey, these are three interior angles in a triangle! That's why $\alpha + \beta+ \gamma = 180\degree$.

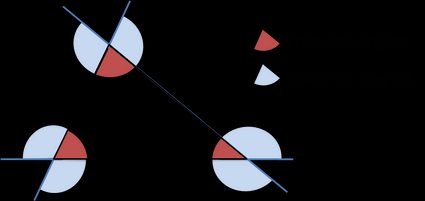
An exterior angle of a triangle is equal to the sum of the opposite interior angles.

• Every triangle has six exterior angles (two at each vertex are equal in measure).
• The exterior angles, taken one at each vertex, always sum up to $360\degree$.
• An exterior angle is supplementary to its adjacent triangle interior angle.

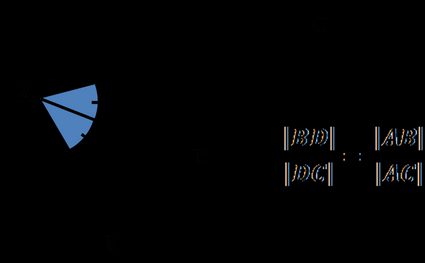
Angle bisector theorem states that:

An angle bisector of a triangle angle divides the opposite side into two segments that are proportional to the other two triangle sides.

Or, in other words:

The ratio of the $\overline{BD}$ length to the $\overline{DC}$ length is equal to the ratio of the length of side $\overline{AB}$ to the length of side $\overline{AC}$:

OK, so let's practice what we just read. Assume we want to find the missing angles in our triangle. How to do that?

1. Find out which formulas you need to use. In our example, we have two sides and one angle given. Choose angle and 2 sides option.
2. Type in the given values. For example, we know that $a = 9\ \mathrm{in}$, $b = 14\ \mathrm{in}$, and $\alpha = 30\degree$. If you want to calculate it manually, use law of sines:

So:

• From the theorem about sum of angles in a triangle, we calculate that $\gamma = 180\degree- \alpha - \beta = 180\degree- 30\degree - 51.06\degree= 98.94\degree$.

3. The triangle angle calculator finds the missing angles in triangle. They are equal to the ones we calculated manually:$\beta = 51.06\degree$, $\gamma = 98.94\degree$; additionally, the tool determined the last side length: $c = 17.78\ \mathrm{in}$.

Reasoning similar to the one we applied in this calculator appears in other triangle calculations, for example the ones we use in the ASA triangle calculator and the SSA triangle calculator!