30 60 90 Triangle Calculator

With this 30 60 90 triangle calculator, you can solve the measurements of this special right triangle. Whether you're looking for the 30 60 90 triangle formulas for the hypotenuse, wondering about the 30 60 90 triangle ratio, or simply want to check what this triangle looks like, you've found the right website. Keep scrolling to learn more about this specific right triangle, or check out our tool for the twin of our triangle – 45 45 90 triangle calc.

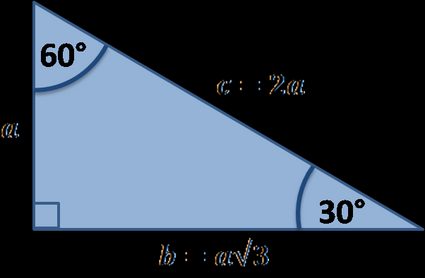
First of all, let's explain what "30 60 90" stands for. When writing about 30 60 90 triangle, we mean the angles of the triangle, that are equal to 30°, 60° and 90°.

Assume that the shorter leg of a 30 60 90 triangle is equal to a. Then:

• The second leg is equal to a√3;
• The hypotenuse is 2a;
• The area is equal to a²√3/2; and
• The perimeter equals a(3 + √3).

The 30 60 90 triangle formulas are quite easy, but what's the math behind them? Let's check which methods you can use to prove them:

1. Using the properties of the equilateral triangle

Did you notice that our triangle of interest is simply half of the equilateral triangle? If you remember the formula for the height of such a regular triangle, you have the answer to what's the second leg length. It's equal to side times a square root of 3, divided by 2:

h = c√3/2, h = b and c = 2a so b = c√3/2 = a√3

2. Using trigonometry

If you are familiar with the trigonometric basics, you can use, e.g., the sine and cosine of 30° to find out the other sides' lengths:

a/c = sin(30°) = 1/2 so c = 2a

b/c = sin(60°) = √3/2 so b = c√3/2 = a√3

Also, if you know two sides of the triangle, you can find the third one from the Pythagorean theorem. However, the methods described above are more useful as they need to have only one side of the 30 60 90 triangle given.

If we know the shorter leg length a, we can find out that:

• b = a√3

• c = 2a

If the longer leg length b is the one parameter given, then:

• a = b√3/3

• c = 2b√3/3

For hypotenuse c known, the legs formulas look as follows:

• a = c/2

• b = c√3/2

Or simply type your given values, and the 30 60 90 triangle calculator will do the rest!

The most important rule to remember is that this special right triangle has one right angle, and its sides are in an easy-to-remember consistent relationship with one another - the ratio is a : a√3 : 2a. Also, the unusual property of this 30 60 90 triangle is that it's the only right triangle with angles in an arithmetic progression.

What is an arithmetic progression? Check our arithmetic sequence calculator to learn more!

In the 30 60 90 triangle the ratios are:

• 1 : 2 : 3 for angles (30° : 60° : 90°); and
• 1 : √3 : 2 for sides (a : a√3 : 2a).

You read about 30 60 90 triangle rules. Now it's high time you practiced!

1. Enter the given value. Let's say we want to check how to solve the 30 60 90 triangle from our triangle set. There's a scale on the longer leg. Assume its length is 11 inches.
2. All the other values appear! Thanks to this 30 60 90 triangle calculator, you find out that:

• The shorter leg is 6.35 in - because a = b√3/3 = 11in × √3/3 ~ 6.35 in.
• The hypotenuse is equal to 12.7 in - because c = 2b√3/3 = 2a ~ 12.7 in.
• The area is 34.9 in² - it's the result of multiplying the legs' length and dividing by 2 area = (a²√3)/2 ≈ 34.9 in².
• The perimeter equals 30.05 in - adding all sides gives that result perimeter = a + a√3 + 2a = a(3 + √3) ≈ 30.05 in.