Special Right Triangles Calculator

Q: What are the formulas for a 45 45 90 triangle?

A 45° 45° 90° triangle has the following formulas, where x is the length of any of the equal sides: Hypotenuse = x√2 ; Area = x²/2 ; and Perimeter = x(2+√2) .

Q: Is 3, 4, and 5 a Pythagorean triplet?

Yes . The integers a = 3 , b = 4 , and c = 5 form a Pythagorean triplet since a² + b² = c² , and a triangle with sides abc is a right special triangle.

Creators

Hanna Pamuła, PhD

Hanna PamułaPhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Reviewers

Bogna Szyk

Bogna is the chief operating officer at Omni Calculator, where she helps keep things running smoothly and ideas moving forward. With a background in civil engineering and a knack for organizing chaos, she brings structure and strategy to everything she does. After hours, you’ll likely find her dancing zouk or crafting the next twist in a D&D campaign. See full profile

Check our editorial policy

and Adena Benn

Adena Benn

Website

Adena Benn is a Guyanese teacher with a degree in computer science who is always reading and learning. She loves problem-solving, everything tech, and working with teenagers. She has a passion for education and is especially interested in how children learn and the teaching methods that best suit their learning styles. She grew up on a farm in Pomeroon, Guyana, where she worked alongside her parents and siblings. As such, she is just as comfortable growing plants as teaching in the classroom. In her early life, she also gained expertise as a seamstress, which she learned from her mother. By grade 9, she had already acquired her dressmaker's certificate. Today she uses her skills to design many items for her family. In her free time, Adena loves to read, take long walks, write children’s stories and poetry, travel, or spend time with her family. See full profile

Check our editorial policy

This special right triangles calculator will help you solve the chosen triangle's measurements in a blink of an eye. Select the triangle you need and type the given values – the remaining parameters will be calculated automatically.

The special right triangles are right triangles for which simple formulas exist. That allows quick calculations, so you don't need to use the Pythagorean theorem or some advanced method. Scroll down to read more about special right triangle formulas and rules.

Special right triangles 30 60 90

The special right triangle $30\degree$ $60\degree$ $90\degree$ is one of the most popular right triangles. Its properties are unique because it's half of the equilateral triangle.

If you want to read more about that special shape, check our dedicated 30° 60° 90° triangle calculator.

Special right triangles 45 45 90

Another famous special right triangle is the $45\degree$ $45\degree$ $90\degree$ triangle. It's the only possible right triangle that is also an isosceles triangle. Also, it's the shape created when we cut the square along the diagonal:

Special right triangle: 45-45-90 with a given leg length.

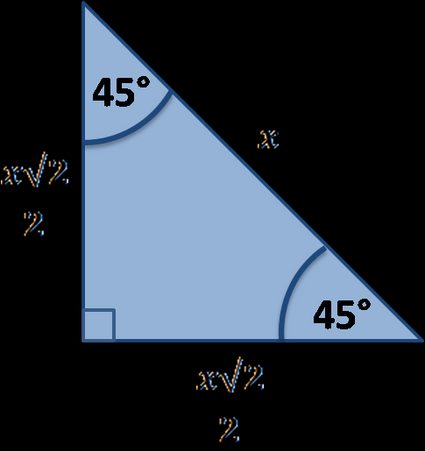
Special right triangle: 45-45-90 with a given hypotenuse length.

Curious about this triangle's properties? Please look at our 45° 45° 90° triangle calculator.

Other special right triangles

Many special right triangles exist, below you'll find the ones implemented in our tool:

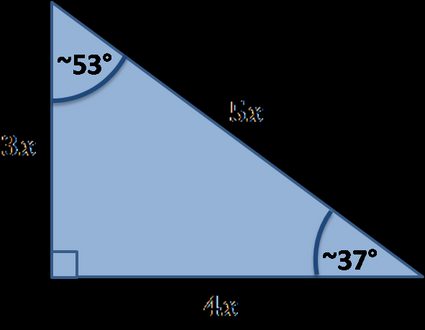
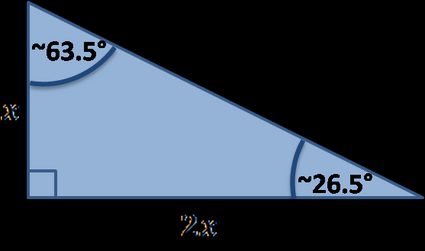
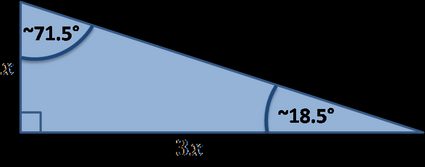
Special right triangles formulas

Right triangle with sides a, b, c and angles α, β.

If you are looking for the formulas for special right triangles, you are in the right place. Look at this neat table below; everything should be clear! In this table, you'll find the formulas for the relationship between special right triangle angles, legs, hypotenuse, area, and perimeter:

Special right triangle	$a$ (shorter leg)	$b$ (longer leg)	$c$ (hypotenuse)	Area	Perimeter	Angle $\alpha$	Angle $\beta$
$30\degree$ - $60\degree$ - $90\degree$	$x$	$x\sqrt 3$	$2x$	$x^2\sqrt{3}/2$	$x(3+\sqrt3)$	$30\degree$	$60\degree$
$45\degree$ - $45\degree$ - $90\degree$	$x$	$x$	$x\sqrt 2$	$x^2/2$	$x(2+\sqrt 2)$	$45\degree$	$45\degree$
$x$ - $2x$	$x$	$2x$	$x\sqrt5$	$x^2$	$x(3+\sqrt 5)$	$\sim26.5\degree$	$\sim63.5\degree$
$x$ - $3x$	$x$	$3x$	$x\sqrt {10}$	$3x^2/2$	$x(4+\sqrt{10})$	$\sim18.5\degree$	$\sim71.5\degree$
$3x$ - $4x$ - $5x$	$3x$	$4x$	$5x$	$6x^2$	$12x$	$\sim37\degree$	$\sim53\degree$

Special right triangle rules

Special right triangles are the triangles that have some specific features which make the calculations easier. Of course, the most important special right triangle rule is that they need to have one right angle plus that extra feature. Generally, special right triangles may be divided into two groups:

Angle-based right triangles – for example $30\degree$ - $60\degree$ - $90\degree$ and $45\degree$ - $45\degree$ - $90\degree$ triangles.
Side-based right triangles – figures that have side lengths governed by a specific rule, e.g.:
- Sides with integer lengths called Pythagorean triplets:
  
  $3:4:5$ , $5:12:13$ , $8:15:17$ , $7:24:25$ , $9:40:41$ …
- Sides with integer lengths but almost-isosceles:
  
  $20:21:29$ , $119:120:169$ , $696:697:985$ …
- Right triangle, the sides of which are in a geometric progression (Kepler triangle). It's formed by three square sides. Their areas are in geometric progression, according to the golden ratio. For more on this special ratio, head to our golden ratio calculator.

There are many different rules and choices by which we can choose the triangle and call it special. In our special right triangles calculator, we implemented five chosen triangles: two angle-based and three side-based.

Special right triangle calculator – example

Let's have a look at the example: we want to find the length of the hypotenuse of a right triangle if the length of one leg is $5$ inches and one angle is $45\degree$ .

Choose the proper type of special right triangle. In our case, it's $45\degree$ - $45\degree$ - $90\degree$ triangle.
Type in the given value. We know that the side is equal to $5$ in, so we type that value in the a or b box – it doesn't matter where because it's an isosceles triangle.
Wow! The special right triangle calculator solved the measurements of your triangle! Now we know that:
- Second leg $b$ is equal to $5\ \mathrm{in}$ ;
- Hypotenuse $c$ is $7.07\ \mathrm{in}$ ;
- Perimeter equals $17.07\ \mathrm{in}$ ; and
- Area of our special triangle is $12.5\ \mathrm{in^2}$ .

Don't wait any longer. Try it yourself!

FAQs

What are the formulas for a 45 45 90 triangle?

A 45° 45° 90° triangle has the following formulas, where x is the length of any of the equal sides:

Hypotenuse = x√2;
Area = x²/2; and
Perimeter = x(2+√2).

How do I solve a 30 60 90 special right triangle?

To solve a 30° 60° 90° special right triangle, follow these steps:

Find the length of the shorter leg. We'll call this x.
The longer leg will be equal to x√3.
Its hypotenuse will be equal to 2x.
The area is A = x²√3/2.
Lastly, the perimeter is P = x(3 + √3).

What are the two special triangles in trigonometry?

30° 60° 90° triangles and 45° 45° 90° (or isosceles right triangle) are the two special triangles in trigonometry. While there are more than two different special right triangles, these are the fastest to recognize and the easiest to work with. An example of a non-angle-based special right triangle is a right triangle whose sides form a Pythagorean triple.

Is 3, 4, and 5 a Pythagorean triplet?

Yes. The integers a = 3, b = 4, and c = 5 form a Pythagorean triplet since a² + b² = c², and a triangle with sides abc is a right special triangle.