Isosceles Triangle Calculator

The isosceles triangle calculator is the best choice if you are looking for a quick solution to your geometry problems. Find the isosceles triangle area, its perimeter, inradius, circumradius, heights, and angles - all in one place. If you want to build a kennel, find out the area of the Greek temple isosceles pediment, or simply do your maths homework, this tool is here for you. Experiment with the calculator or keep reading to find out more about the isosceles triangle formulas and the isosceles triangle theorem.

An isosceles triangle is a triangle with two sides of equal length, called legs. The third side of the triangle is called the base. The vertex angle is the angle between the legs. The angles with the base as one of their sides are called the base angles.

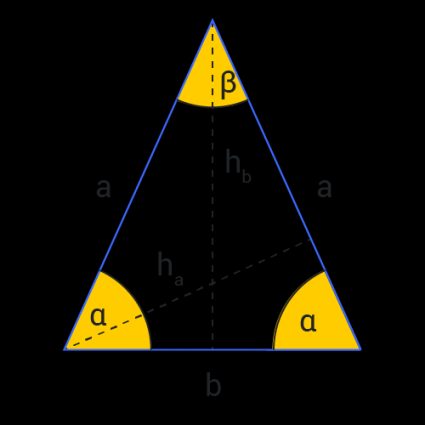
Here are the most important properties of isosceles triangles:

• It has an axis of symmetry along its vertex height;
• The two angles opposite the legs are equal; and
• The isosceles triangle can be acute, right, or obtuse, but it depends only on the vertex angle (base angles are always acute)

The equilateral triangle is a special case of an isosceles triangle. You can learn about all the possible types of triangles in the classifying triangles calculator. Additionally, if you wish to delve further into the characteristics of an equilateral triangle, check out equilateral triangle calculator

To calculate the isosceles triangle area, you can use many different formulas. The most popular ones are the equations:

1. Given leg a and base b:

   area = (1/4) × b × √( 4 × a² - b² )

2. Given h height from apex and base b or h2 height from the other two vertices and leg a:

   area = 0.5 × h × b = 0.5 × h2 × a

3. Given any angle and leg or base

   area = (1/2) × a × b × sin(base_angle) = (1/2) × a² × sin(vertex_angle)

Also, you can check our triangle area calculator to find other equations, which work for every type of triangle, not only for the isosceles one.

To calculate the isosceles triangle perimeter, simply add all the sides of the triangle:
perimeter = a + a + b = 2 × a + b

Isosceles triangle theorem, also known as the base angles theorem, claims that if two sides of a triangle are congruent, the angles opposite to these sides are congruent.

Also, the converse theorem exists, stating that if two angles of a triangle are congruent, then the sides opposite those angles are congruent.

A golden triangle, which is also called a sublime triangle, is an isosceles triangle in which the leg is in the golden ratio to the base:

a / b = φ ~ 1.618

The golden triangle has some unusual properties:

• It's the only triangle with three angles in 2:2:1 proportions
• It's the shape of the triangles found in the points of pentagrams
• It's used to form a logarithmic spiral

Let's find out how to use this tool with a simple example. Have a look at this step-by-step solution:

1. Determine what is your first given value. Assume we want to check the properties of the golden triangle. Type 1.681 inches into the leg box.
2. Enter second known parameter. For example, take a base equal to 1 in.
3. All the other parameters are calculated in the blink of an eye! We checked, for instance, that the isosceles triangle perimeter is 4.236 in and that the angles in the golden triangle are equal to 72° and 36° - the ratio is equal to 2:2:1, indeed.

You can use this calculator to determine different parameters than in the example, but remember that there are generally two distinct isosceles triangles with a given area and other parameters, e.g., leg length. Our calculator will show one possible solution.