Golden Ratio Calculator

The golden ratio calculator will calculate the shorter side, longer side, and combined length of the two sides to compute the golden ratio. Before we can calculate the golden ratio, it's important to answer the question, "what is the golden ratio?". The following article hopes to provide you with an answer.

You can also check out the proportion calculator if you want to analyze ratios in general.

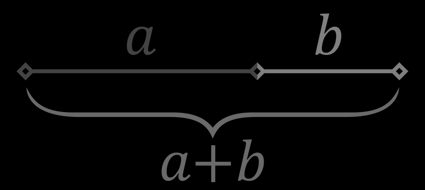
The golden ratio, also known as the golden section or golden proportion, is obtained when two segment lengths have the same proportion as the proportion of their sum to the larger of the two lengths. The value of the golden ratio, which is the limit of the ratio of consecutive Fibonacci numbers, has a value of approximately $1.618$.

The formula for the golden ratio is as follows. Let the larger of the two segments be $a$, and the smaller be denoted as $b$ The golden ratio is then $\small (a+b)/a = a/b$ Any old ratio calculator will do this trick for you, but this golden ratio calculator deal with this issue specifically so you don't have to worry!

Here's a step-by-step method to solve the ratio by hand.

1. Find the longer segment and label it $a$.

2. Find the shorter segment and label it $b$.

3. Input the values into the formula.

4. Take the sum $a$ and $b$ and divide by $a$.

5. Take $a$ divided by $b$.

6. If the proportion is in the golden ratio, it will equal approximately $1.618$.

7. Use the golden ratio calculator to check your result.

The segment addition postulate calculator can be used to find one of the segment lengths when 3 points are collinear, and two of the distances are known.

The golden rectangle is a rectangle with a length of $a+b$ and width of $a$. This rectangle is often seen in art, as it has been said it's the most pleasing to the eye of all such rectangles. The golden rectangle calculator is a convenient way to find the golden rectangle instead of working it by hand.

The golden ratio is seen in many forms of architecture and in some patterns of nature, such as in the arrangement of leaves in some plants. The golden proportion is also seen in regular pentagons. You can find more information about this shape in the pentagon calculator.

The golden ratio is a ratio between two quantities that we can also find when we compute the ratio between the sum of these quantities and the greater of the two. Numerically speaking, the number a and b are in the golden ratio if:

a/b = (a + b)/a

This ratio has a specific value, denoted by the Greek letter φ:

φ = 1.618033988749

The golden ratio is highly regarded as figures built following these proportions look particularly pleasant to the human eye.

The sides of a golden rectangle with diagonal d = 1 are a = 0.850651 and b = 0.525731. To find these results:

1. Use Pythagoras' theorem to find the length of the side b as a function of a:

   b = sqrt(1 - a²).

2. Compute the length of the side a knowing that a/b = φ:

   a/b = φ
a/sqrt(1 - a²) - φ
a = sqrt(φ²/(1 + φ²)) = 0.850651

3. Compute the length of side b with the following formula:

   b = a/φ = 0.525731

That's it!

The golden ratio has always had particular relevance in science and art thanks to its properties and appearance. Talking about math:

• A golden rectangle (a rectangle whose sides are in golden ratio) can be split into two smaller golden rectangles (it maintains its proportions).
• The golden ratio deeply correlates with the number 5. This number appears in its definition (φ = (1 + √5)/2) and the pentagon as the ratio between diagonal and side.

In arts, the golden ratio appeared more recently: Dalí, for example, used this ratio in its works.

Many sources, both historical and contemporary, claim that the golden ratio is rather ubiquitous in Nature. Some examples are:

• The growth pattern of leaves;
• The geometrical surfaces of some vegetables and shells;
• The proportions of some animals' bones.

However, while we can't deny the presence of geometrical patterns in nature, we can't confirm the exactness of the proportions of the examples above: some present huge variations, while others only approximate the golden ratio.