Ratio Calculator

The ratio calculator will help you compute identical ratios given three of the four parts of the two ratios. A ratio is a relationship between two quantities, very often represented as a fraction. It displays how much of one part is contained in another part, basically representing a fractional or percentage amount of the whole.

Before we can use the calculator, we need to understand how to do ratios and how to find a ratio.

A ratio is made up of two parts, the same as how a fraction is made up of two parts. There is the numerator (the top number of the fraction) and the denominator (the bottom number of the fraction).

For example, suppose there is a pie cut into eight slices and three of the eight slices have been eaten. If we want to know the ratio of slices eaten compared to the entire pie, then we have to put the number eaten as the numerator and the total number of pieces as the denominator; 3/8.

That is the most basic of ratios since no simplification is involved. But what if we want to simplify or scale up the ratio to a larger, yet equivalent ratio? The next section on how to find a ratio will explain the process.

Suppose we have the same ratio of 3/8, but we want to scale it up to a larger, equivalent ratio with a denominator of 72. The way to do this is to set up a proportion, which is two ratios equal to each other and solve for the missing part. We can do this as follows:

1. Write both ratios in terms of fractions, labeling the missing part with an x.
2. Set the fractions equal to each other, forming a proportion.
3. Use the process of cross-multiplication to isolate the variable.
4. Solve for the variable.
5. Use the ratio calculator to check your answer.

In the above example, the steps would look as follows:

1. 3/8 = x/72;
2. 8 · x = 72 · 3;
3. 8x = 216;
4. x = 27.

For more complex ratios involving larger numbers or decimals, the ratio calculator is much more convenient to use. The proportion calculator, which does the same thing, may also be used to solve problems such as the one above.

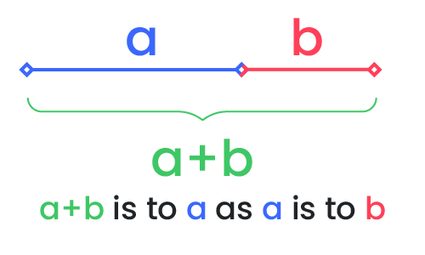
The golden ratio is a special ratio that is achieved when two quantities have the same ratio as the ratio of their sum to the larger of the two quantities. If we denote the two quantities at a and b, then the golden ratio is (a+b)/a = a/b. The value of this ratio is approximately 1.618. The golden ratio calculator is handy for computing this ratio.

It has been said that the rectangle that is most aesthetically pleasing to the eye is the golden rectangle. This is a rectangle with length a + b and width a. The rectangle is golden if (a+b)/a = a/b. The golden rectangle calculator will compute the length and width necessary to achieve the perfect golden rectangle.

The ratio calculator is also helpful in the geometric application of similar triangles. If the sides of one triangle are in proportion with the sides of another triangle, the two triangles are said to be similar. This applies to other polygons as well.