45 45 90 Triangle Calculator

45 45 90 triangle calculator is a dedicated tool to solve this special right triangle. Find out what are the sides, hypotenuse, area, and perimeter of your shape and learn about the 45 45 90 triangle formulas and ratios. We'll also discuss the 45 45 90 triangle rules that are most probable to come up in your homework assignments. Never again will you wonder how to solve a 45 45 90 triangle!

If you want to know more about other popular right triangles, check out this 30 60 90 triangle calculator and the special right triangles calculator.

Do you need formulas for the 45 45 90 triangle? You're in the right place! If the leg of the triangle is equal to a, then:

• The second leg is also equal to a;
• The hypotenuse is a√2;
• The area is equal to a²/2; and
• The perimeter equals a(2 + √2).

OK, these 45 45 90 triangle formulas look easy, but where do they come from? There are a couple of methods to prove them, the most popular of them are:

1. Using the Pythagorean theorem

• As you know one leg length a, you the know the length of the other as well, as both of them are equal.

• Find the hypotenuse from the Pythagorean theorem: we have a² + b² = c² and a = b, so

  a² + a² = c²

  which gives

  c = √(2a²) = a√2

2. Using the properties of the square

Did you notice that the 45 45 90 triangle is half of a square, cut along the square's diagonal?

• Again, we know that both legs are equal to a.
• As you probably remember, the diagonal of the square is equal to side times square root of 2, that is a√2. In our case, this diagonal is equal to the hypotenuse. That was quick!

3. Using trigonometry

If you know trigonometry, you could use the properties of sine and cosine. For this special angle of 45°, both of them are equal to √2/2. So:
a/c = √2/2 so c = a√2

To find the area of the triangle, use the basic triangle area formula, which is area = base × height / 2. In our case, one leg is a base, and the other is the height, as there is a right angle between them. So the area of 45 45 90 triangles is:

area = a² / 2

To calculate the perimeter, simply add all 45 45 90 triangle sides:

perimeter = a + b + c = a + a + a√2 = a(2 + √2)

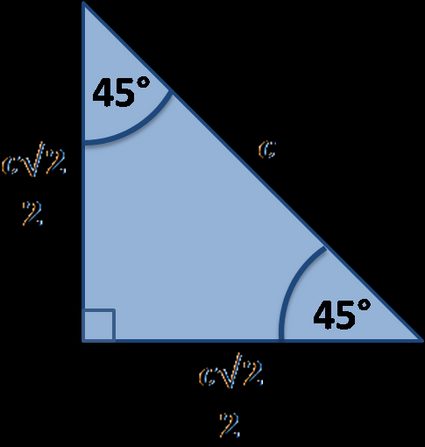
The legs of such a triangle are equal; the hypotenuse is calculated immediately from the equation c = a√2. If the hypotenuse value is given, the side length will be equal to a = c√2/2.

The most important rule is that this triangle has one right angle, and two other angles are equal to 45°. It implies that two sides —legs— are equal in length, and you can calculate the hypotenuse easily. The other interesting properties of the 45 45 90 triangles are:

• It's the only possible right triangle that is also an isosceles triangle;
• Of all right triangles, it has the smallest ratio of the hypotenuse to the sum of the legs; and
• Of all right triangles, it has the greatest altitude ratio from the hypotenuse to the sum of the legs.

In a 45 45 90 triangle, the ratios are equal to:

• 1 : 1 : 2 for angles (45° : 45° : 90°); and
• 1 : 1 : √2 for sides (a : a : a√2).

Have a look at this real-life example to catch on the 45 45 90 triangle rules.

Assume we want to solve the isosceles triangle from a triangle set.

1. Type the given value. In our case, the easiest way is to type the length of the part with the scale. The usual leg length is 9 inches, so type that value into the a or b box.
2. The 45 45 90 triangle calculator shows the remaining parameters. Now you know:

• hypotenuse length — 9 in × √2 = 12.73 in;
• area — 9 in × 9 in / 2 = 40.5 in²; and
• perimeter — 9 in + 9 in + 9 in × √2 = 30.73 in.

Remember that you can change the units displayed by simply clicking on the unit name. Also, don't forget that our 45 45 90 triangle calculator is a flexible tool - if you only know the area, the hypotenuse, or even the perimeter, it can calculate the remaining parameters as well. Awesome!