Right Triangle Calculator

The right triangle calculator will help you find the lengths of the sides of a right-angled triangle. This triangle solver will also teach you how to find the area of a right triangle as well as give plenty of information about the practical uses of a right triangle.

First things first, let's explain what a right triangle is. The definition is very simple and might even seem obvious for those who already know it: a right-angled triangle is a triangle where one and only one of the angles is exactly 90°. The other two angles will clearly be smaller than the right angle because the sum of all angles in a triangle is always 180°.

In a right-angled triangle, we define the sides in a special way. The side opposing the right angle is always the biggest in the triangle and receives the name of "hypotenuse". The other two sides are called catheti. The relationship between the hypotenuse and each cathetus is straightforward, as we will see when we talk about Pythagoras' theorem.

If all you want to calculate is the hypotenuse of a right triangle, this page and its right triangle calculator will work just fine. However, we would also recommend using the dedicated tool we have developed at Omni Calculators: the hypotenuse calculator. The hypotenuse is opposite the right angle and can be solved by using the Pythagorean theorem. In a right triangle with cathetus a and b and with hypotenuse c, Pythagoras' theorem states that: a² + b² = c².

To solve for c, take the square root of both sides to get c = √(b²+a²). We can consider this extension of the Pythagorean theorem as a "hypotenuse formula". A Pythagorean theorem calculator is also an excellent tool for calculating the hypotenuse.

Let's now solve a practical example of what it would take to calculate the hypotenuse of a right triangle without using any calculators available at Omni:

1. Obtain the values of a and b.
2. Square a and b.
3. Sum up both values: a² + b².
4. Take the square root of the result.
5. The square root will yield positive and negative results. Since we are dealing with length, disregard the negative one.
6. The resulting value is the value of the hypotenuse c.

Now let's see what the process would be using one of Omni's calculators, for example, the right triangle calculator on this web page:

1. Insert the value of a and b into the calculator; and
2. Obtain the value of c immediately;
3. As a bonus, you will get the value of the area for such a triangle.

We have already seen that calculating the area of a right angle triangle is very easy with the right triangle calculator. At Omni Calculators, we have a calculator specifically designed for that purpose as well: area of a right triangle calculator. Let's now see a bit more in-depth how to calculate areas of right triangles.

The method for finding the area of a right triangle is quite simple. All that you need are the lengths of the base and the height. In a right triangle, the base and the height are the two sides that form the right angle. Since multiplying these two values together would give the area of the corresponding rectangle, and the triangle is half of that, the formula is:

area = ½ × base × height.

If you don't know the base or the height, you can find it using the Pythagorean theorem. Try the right triangle calculator to check your calculations or calculate the area of triangles with sides that have larger or decimal-value lengths.

Now we're gonna see other things that can be calculated from a right triangle using some of the tools available at Omni. The sides of a triangle have a certain gradient or slope. The formula for the slope is

slope = (y₂ - y₁)/(x₂ - x₁).

So if the coordinates are (1,-6) and (4,8), the slope of the segment is (8 + 6)/(4 - 1) = 14/3. An easy way to determine if the triangle is right, and you just know the coordinates, is to see if the slopes of any two lines multiply to equal -1.

There is an easy way to convert angles from radians to degrees and degrees to radians with the use of the angle conversion:

• If an angle is in radians – multiply by 180/π; and
• If an angle is in degrees – multiply by π/180.

Sometimes you may encounter a problem where two or even three side lengths are missing. In such cases, the right triangle calculator, hypotenuse calculator, and method on how to find the area of a right triangle won't help. You have to use trigonometric functions to solve for these missing pieces.

The right triangle is just one of the many special triangles that exist. These triangles have one or several special characteristics that make them unique. For example, as we have seen, the right triangle has a right angle and hence a hypotenuse, which makes it a unique kind of triangle. Aside from the right-angled triangle, there are other special triangles with interesting properties.

One of the most known special triangles is the equilateral triangle, which has three equal sides and all its angles are 60°. This makes it much simpler to make a triangle solver calculator evaluate different parameters of such a triangle.

Another of special triangles is the isosceles triangle, which has 2 sides of equal length, and hence two angles of the same size. As opposed to the equilateral triangle, isosceles triangles come in many different shapes.

There are many other special triangles. However, we will now take a look at a few very special right triangles that, besides being right-angled triangles, they have other unique properties that make them interesting.

The so-called "45 45 90" triangle is probably the most special among all the special right triangles. This is a right-angled triangle that is also an isosceles triangle. Both its catheti are of the same length (isosceles), and it also has the peculiarity that the non-right angles are exactly half the size of the right angle that gives the name to the right triangle.

This right triangle is the kind of triangle that you can obtain when you divide a square by its diagonal. That is why both catheti (sides of the square) are of equal length. For those interested in knowing more about the most special of the special right triangles, we recommend checking out the 45 45 90 triangle calculator made for this purpose.

Another fascinating triangle from the group of special right triangles is the so-called "30 60 90" triangle. The name comes from having one right angle (90°), then one angle of 30°, and another of 60°. These angles are special because of the values of their trigonometric functions (cosine, sine, tangent, etc.). The consequences of this can be seen and understood with the 30 60 90 triangle calculator, but for those who are too lazy to click the link, we will summarize some of them here. Assuming that the shorter side is of length a, the triangle follows:

1. The second length is equal to a√3;
2. The hypotenuse is 2a;
3. The area is equal to (a²√3)/2; and
4. The perimeter equals a(3 + √3).

It might seem at first glance that a right triangle and a parallelogram do not have anything in common. How can a triangle solver help you understand a parallelogram? The reality is that any parallelogram can be decomposed into 2 or more right triangles. Let's take an example of the rectangle, which is the easiest one to see it.

Imagine a rectangle, any rectangle. Now draw a trace on one of the diagonals of this rectangle. If we separate the rectangle by the diagonal, we will obtain two right-angled triangles. Looking at the triangles, there is no need to use the right triangle calculator to see that both are equal, so their areas will be the same. This means that the area of the rectangle is double that of each triangle.

If we think about the equations, it makes sense since the area of a rectangle of sides a and b is exactly area = a × b, while for the right triangle is area = base × height / 2 which, in this case, would mean area = a × b /2. This is precisely what we already saw by just cutting the rectangle by the diagonal.

It was a simple example of a rectangle, but the same applies to the area of a square. For other parallelograms, the process becomes a bit more complicated (it might involve up to 4 right triangles of different sizes). Still, with a bit of skill, you can use the same idea and calculate the area of a parallelogram using right-angled triangles. You can, of course, be even more efficient and just use our calculator.

Geometry and polygons, especially triangles, always come together. The properties of some triangles, like right triangles, are usually interesting and shocking, even for non-mathematicians. We will now have a look at an interesting set of numbers very closely related to right-angled triangles that mathematicians love, and maybe you will too.

These sets of numbers are called the Pythagorean triplets and are sets of 3 integers (let's call them a, b, and c) and satisfy the Pythagorean theorem: a² + b² = c². That is, they could form a right triangle with sides of length a, b, and c. The amount of numbers that satisfy this relationship is limited, but mathematicians find joy in searching for new ones.

Aside from the curiosity factor of this relationship, it has some interesting properties that are exploited in cryptography. Given the applications that one might find for such sets of numbers, mathematicians have explored even beyond, using 4, 5… and more sets of numbers that satisfy a similar relation in which the sum of the squares of all the numbers except for one, give the square of the number that's left.

Also very connected to these Pythagorean triplets is the infamous Fermat's last theorem in which the almost legendary cryptic mathematician Pierre Fermat stated that there could not be a set of three integer numbers that would satisfy the relation: aⁿ + bⁿ = cⁿ for n bigger than 2. This conjecture was only proven in 1995, more than 300 years after it was first formulated, and it's considered one of the most important mathematical problems of the century.

We have talked a lot about triangles, particularly right triangles, and their applications in maths and geometry. What we haven't talked about yet is the usefulness of right triangles for calculating things in real life. It might seem like the applications outside of geometry are limited, but let's have a look at shadows.

Yes, shadows. The dark shade projected by an object when it is illuminated. If you were to look at the shape made by the shadow, the object, and the ground, you would notice that it is, in fact, a right-angled triangle! At least, it is when the object is perfectly vertical and the ground is horizontal. Most of the time, this is the case, or at least close enough. This means that we can use the right triangle calculator to find different pieces of information about objects under the sun. Let's see how.

Imagine that you have a building of which we want to know the height, but you cannot measure it directly because it's too high to drop a measuring tape from the top. What you can do is measure the length of the shadow on the street. Then, with the help of any angle-measuring tool and a piece of paper, you can find out the angle between the shadow and the ground. Knowing that the angle between the building and the ground is 90°, you can obtain the value of the height of the building.

Using this technique, you can measure the height of many objects as long as you have a bright sunny day or other light sources to illuminate the object. In fact, this used to be a very common measuring technique in the olden days. Probably the most interesting and mind-blowing use of right triangles is that of Eratosthenes, who managed to use right-angled triangles and shadows to measure the radius of the Earth, and now we are gonna explain how he did it.

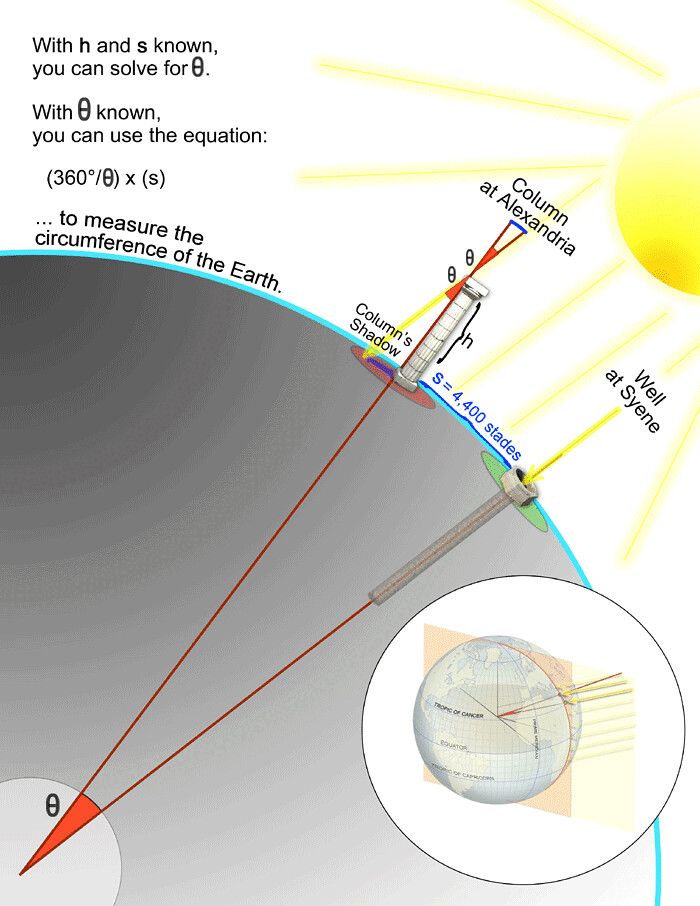
Eratosthenes noticed that on the summer solstice there was a place on Earth where the wells did not have a shadow at midday, i.e., the sun shone straight down onto them. Noting this, he set up a column of a known height at a known distance from that well and measured the size of the shadow created by the pole at noon on the solstice day. Then using right-angled triangles and trigonometry, he was able to determine the angle going from the center of the Earth between the well and the pole, as well as the radius of the Earth, based on the known distance between these two points.

It was quite an astonishing feat that now you can do much more easily, by just using the Omni calculators that we have created for you.