Area of a Right Triangle Calculator

Q: What is the area of a right triangle with hypotenuse 5 cm and angle 45°?

The area is 6.25 . We get this answer by applying the formula area = c² × sin(α) × cos(α) / 2 with c = 5 and α = 45° . The math theorem used to derive this formula is called the law of sines .

Q: What do we call the sides of a right triangle?

The two sides perpendicular to each other are called legs . The side opposite the right angle (in other words, the longest side) is the hypotenuse .

Creators

Hanna Pamuła, PhD

Hanna PamułaPhD

Website

Research Gate

Hanna (Hania) Pamuła holds a Ph.D. in Bioacoustics / Mechanical Engineering, obtained at AGH University of Science and Technology. She has participated in research work in labs in France and the UK and presented papers at several international conferences. Hania has a penchant for photography and graphic design. When not in the office, she’s probably traveling, hiking, or out in the field, watching birds and recording their calls. See full profile

Check our editorial policy

Reviewers

Bogna Szyk

Bogna is the chief operating officer at Omni Calculator, where she helps keep things running smoothly and ideas moving forward. With a background in civil engineering and a knack for organizing chaos, she brings structure and strategy to everything she does. After hours, you’ll likely find her dancing zouk or crafting the next twist in a D&D campaign. See full profile

Check our editorial policy

If you are wondering how to find the right triangle area, you're in the right place – this area of a right triangle calculator is the tool for you.

Whether you're looking for the equation given triangle legs, leg, and the hypotenuse, or side and angle, you won't be disappointed – this calculator has all of them implemented.

Please scroll down to learn more about the area of right triangle formulas, or simply give our calculator a try!

Area of right triangle formulas

🙋 If you've just noticed that your triangle is not a right triangle, check out this general triangle area calculator.

The basic equation is a transformed version of a standard triangle height formula ( $a \cdot h / 2$ ). Because the right triangle legs are perpendicular to each other, one leg is taken as a base, and the other is a right triangle height:

\text{area}=\frac{a\cdot b}{2}

Sometimes it's not so obvious – you have other values given, not two legs. Then what?

If you have one leg and hypotenuse given, use the Pythagorean theorem to find the missing leg:

\qquad a^2+b^2=c^2

Then calculate the square root of the transformed equation:

Given $a$ and $c$ we find that $b = \sqrt{c^2 - a^2}$ :

\qquad\text{area}=a\cdot\frac{\sqrt{c^2-a^2}}{2}

Given $b$ and $c$ we calculate that $a = \sqrt{c^2 - b^2}$ :

\qquad \text{area} = b\cdot\frac{\sqrt{c^2-b^2}}{2}

If you know one angle and hypotenuse, you can calculate the law of sines on this triangle:

\qquad a=c\cdot\sin(\alpha)

Hence:

\qquad \begin{split} b&=c\cdot\sin(\beta)\\&=c\cdot\sin(90\degree-\alpha)\\ &=c\cdot\cos(\alpha) \end{split}

Thus:

\qquad \text{area}=c^2\cdot\sin(\alpha)\cdot\frac{\cos(\alpha)}{2}

Given one angle and one leg, find the area using e.g. trigonometric functions:

\qquad\frac{a}{b}=\tan(\alpha)

And:

\qquad\frac{b}{a}=\tan(\beta)

We find:

\qquad \begin{split} \text{area}&=b\cdot\tan(\alpha)\cdot\frac{b}{2}\\ \\[1.5em] &=b^2\cdot\frac{\tan(\alpha)}{2} \end{split}

Or:

\qquad \begin{split} \text{area}&=a\cdot a\cdot \frac{\tan(\beta)}{2}\\[1em] &=a^2\cdot\frac{\tan(\beta)}{2} \end{split}

🙋 Do you want to know more about right triangles? Visit our right triangle calculator!

Area of an isosceles right triangle

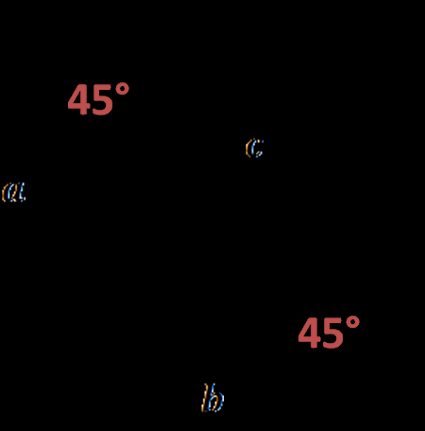
An isosceles right triangle is a special right triangle, sometimes called a 45-45-90 triangle (it's so special we made a tool just for it, the 45 45 90 triangle calculator). In such a triangle, the legs are equal in length (as a hypotenuse always must be the longest of the right triangle sides):

a=b

One leg is a base, and the other is the height – there is a right angle between them. So the area of an isosceles right triangle is:

\text{area}=\frac{a^2}{2}

How to use the area of a right triangle calculator

Let's show the step-by-step calculation:

Pick one option, depending on what you are given. Assume that we know one leg and angle, so we change the selection to given angle and one side.
Enter the values. For example, we know that $\alpha = 40\degree$ and $b$ is $17\ \text{in}$ .
Watch our area of a right triangle calculator performing all calculations for you! The area of the chosen triangle is $121.25\ \text{in}^2$ .

FAQs

How do I find the area of a right triangle given sides?

The method depends on which sides you're given:

If you know the two legs, then use the formula area = a × b / 2, where a, and b are the legs.
If you know one leg a and the hypotenuse c, use the formula: area = a × √(c² - a²) / 2.

What is the area of a right triangle with hypotenuse 5 cm and angle 45°?

The area is 6.25. We get this answer by applying the formula area = c² × sin(α) × cos(α) / 2 with c = 5 and α = 45°. The math theorem used to derive this formula is called the law of sines.

How do I know if it is a right triangle?

If you're given three sides of a triangle and want to know if this triangle is right, check if the Pythagorean formula holds: a² + b² = c², where c is the longest side and a, and b are two other sides.

What do we call the sides of a right triangle?

The two sides perpendicular to each other are called legs. The side opposite the right angle (in other words, the longest side) is the hypotenuse.