Last updated: Jul 22, 2024

Heron's Formula Calculator

Q: How to find 's' in the Heron's formula?

The s in Heron's formula is the triangle's semiperimeter . It is equal to half the perimeter of the triangle. For a triangle with sides a , b , and c , the s is given as: s = (a+b+c)/2

Q: How do you calculate Heron's formula?

To calculate the area of a triangle with sides a , b , and c using Heron's formula, follow these steps: Calculate the triangle's semiperimeter s : s = (a+b+c)/2 Subtract each side from this semiperimeter and multiply each result together: (s-a)⋅(s-b)⋅(s-c) . Multiply this result by the semiperimeter: s⋅(s-a)⋅(s-b)⋅(s-c) . Take the square root of this value to get the area of the triangle: A = √(s⋅(s-a)⋅(s-b)⋅(s-c)) Verify your result with Omni's Heron's formula calculator.

Q: Does Heron's formula always work?

Heron's formula usually works but breaks down for very thin triangles with tiny angles. When one side ( c ) of a triangle is very small, and the other two sides ( a, b ) are approximately equal to the semiperimeter s , the values (s-a) and (s-b) will be very small, leading to numerical instability. In such cases, we can use the following alternative formula for better numerical stability in floating-point arithmetic: A = ¼⋅√((a+b+c)⋅(-a+b+c)⋅(a-b+c)⋅(a+b-c))

New

Table of contents

Heron's area formula: equation for the area of triangle with 3 sides given Heron's formula proof How to use Heron's formula calculator?FAQs

If you are wondering how to calculate the area of a triangle knowing its three sides, you're in the right place – this Heron's formula calculator can do it in no time. Simply type in your values – e.g., triangle side lengths – and our tool will show you the answer.

If you're curious about Heron's area formula, you will read about it below. Also, you may find the proof of Heron's formula there, so keep scrolling to learn more about this useful but not-so-well-known formula.

If you wish to calculate the triangle area normally, head to our triangle area calculator instead.

Heron's area formula: equation for the area of triangle with 3 sides given

Heron's formula, also known as Hero's formula, is the formula to calculate triangle area given three triangle sides. It was first mentioned in Heron's book Metrica, written in ca. 60 AD, which was the collection of formulas for various objects' surfaces and volumes calculation. The basic formulation is:

\footnotesize A = \sqrt{s(s-a)(s-b)(s-c)},

where $s$ is the semiperimeter – half of the triangle perimeter:

\footnotesize s = \frac{a+b+c}{2}.

However, other forms of this formula exist – if you don't want to calculate the semiperimeter by hand, you can use the formula with side lengths only:

\footnotesize A = \frac{1}{4} \sqrt{\begin{split}(a+b+c)(-a+b+c) \ \times \ \\(a-b+c)(a+b-c)\end{split}}

\footnotesize A = \frac{1}{4}\sqrt{4a^2b^2 - (a^2 + b^2 - c^2)^2}

Our perimeter of a triangle calculator can aid you in the perimeter calculator here.

Heron's formula proof

There are many ways to prove Heron's area formula, but you need to know some geometry basics. You can use:

Algebra and the Pythagorean theorem; or
Trigonometry and the law of cosines. For a refresher on this law, visit our law of cosines calculator.

Other proofs also exist, but they are more complex, or they use laws that are not so popular (such as a trigonometric proof using the law of cotangents).

Algebraic proof

In this proof, we need to use the formula for the area of a triangle:

\footnotesize A = \frac{ch}{2}

All the values in the formula should be expressed in terms of the triangle sides: $c$ is a side so it meets the condition, but we don't know much about our height $h$ . So to derive Heron's formula proof, we need to find the $h$ in terms of the sides.

From the Pythagorean theorem, we know that:

\footnotesize \qquad \begin{split} h^2 + (c - d)^2 &= a^2\quad {\rm and}\\[.8em] h^2 + d^2 &= b^2, \end{split}

according to the figure above.

Subtracting those two equations gives us:

\footnotesize \qquad c^2 - 2cd = a^2 - b^2,

from which you can derive the formula for $d$ in terms of the sides of the triangle:

\footnotesize \qquad d = \frac{-a^2 + b^2 + c^2}{2c}

Next step is to find the height in terms of triangle sides. Use the Pythagorean theorem again:

\footnotesize \quad\ \begin{split} h^2 &= b^2 - d^2\\ &= b^2\! -\! \left(\frac{-a^2 + b^2 + c^2}{2c}\right)^2 \end{split}

It's already in terms of the sides, but let's try to reduce it to a nicer form, applying the difference of squares identity:

\! \footnotesize \begin{split} h^2 \! &=\! \frac{(2bc\! -\! a^2\! +\! b^2\! +\! c^2)(2bc\! +\! a^2\! -\! b^2\! -\! c^2)}{4c^2}\\[1em] &=\! \frac{\left((b+c)^2-a^2\right)\left(a^2-(b-c)^2\right)}{4c^2}\\[1em] &=\! \begin{split}(b&+c-a)(b+c+a) \ \times \\& \ (a+b-c)(a-b+c)/ 4c^2\end{split} \end{split}

Apply this formula to the first equation, the one for triangle area:

\footnotesize \begin{split} &A = \frac{ch}{2} = 0.5ch\\[1em] &= 0.5c \ \sqrt{\begin{split}(b&+c-a)(b+c+a) \ \times \\&(a+b-c)(a-b+c) / 4c^2 \end{split}}\\[1em] &= \frac{1}{4} \ \sqrt{\begin{split} (b&+c-a)(b+c+a) \ \times \\& \ (a+b-c)(a-b+c)\end{split}} \end{split}

Here you are! That's the Heron's area proof. Changing the final equation into the form using the semiperimeter is a trivial task.

Trigonometric proof

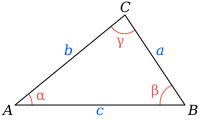
Have a look at the picture – $a$ , $b$ , $c$ are the sides of the triangle, and $\alpha$ , $\beta$ , $\gamma$ are the angles opposing these sides. To find the proof of Heron's formula with trigonometry, we need to use another triangle area formula – given two sides and angle between them:

\footnotesize A = \frac{1}{2}ab\sin(\gamma)

To derive the proof for Heron's formula in this case, we need to express the sine of the angle in terms of the triangle sides. We can use the law of cosines:

\footnotesize \qquad c^2 = a^2 + b^2 - 2ab\cos(\gamma)

Thanks to this law, we get the side-dependent cosine. But how to find the formula for the sine? That's easy; just use the basic relation between the sine and cosine functions – Pythagorean trigonometric identity:

\ \footnotesize \sin^2(\gamma) + \cos^2(\gamma) = 1,

so the formula for cosine is:

\ \footnotesize \begin{split} \sin(\gamma) &= \sqrt{1 - \cos^2(\gamma)}\\[1em] &= \frac{\sqrt{4a^2b^2-(a^2+b^2-c^2)^2}}{2ab} \end{split}

Now you can substitute the sine in the triangle area formula:

\footnotesize \begin{split} A\! &=\! \frac{1}{2}ab\sin(\gamma)\\[1em] &=\! \frac{1}{4}\sqrt{4a^2b^2 - (a^2 + b^2 -c^2)^2}\\[1em] &=\! \frac{1}{4}\sqrt{\begin{split}\left[2ab - (a^2+b^2-c^2)\right] \ \times \\ \left[2ab+(a^2 + b^2 - c^2)\right]\end{split}}\\[1em] &=\! \frac{1}{4}\sqrt{\! \begin{split}& \left[c^2 - (a - b)^2\right] \ \times \\ & \quad \left[-c^2 + (a + b)^2\right]\end{split}}\\[1em] &= \frac{1}{4}\sqrt{\begin{split} (c &-a+b)(c+a-b) \ \times\\&(-c+a-b)(c-a+b)\end{split}} \end{split}

Great! Now you understand why this formula is valid, so don't wait any longer and give Heron's formula calculator a try!

How to use Heron's formula calculator?

It's really easy! Just follow those two simple steps:

Type the given values into the proper boxes. Let's assume that a = 12 in, b = 5 in, and c = 13 in.
The unknown value appears in no time! In our example, the triangle area is the missing value that we want to find. The Heron's formula calculator found out that the area of such a triangle is equal to 30 in².

Remember that in almost every calculator, you can change the units with a simple click on the unit name.

Also, you can use our tool to find out the missing side of the triangle, knowing two sides and the area. However, two such triangles exist which fulfill the condition, so we are showing only one solution – for example, triangles with sides 12, 13, 5 and 12, 13, 24.515 will have the same area equal to 30.

FAQs

How to find 's' in the Heron's formula?

The s in Heron's formula is the triangle's semiperimeter. It is equal to half the perimeter of the triangle.

For a triangle with sides a, b, and c, the s is given as:
s = (a+b+c)/2

How do you calculate Heron's formula?

To calculate the area of a triangle with sides a, b, and c using Heron's formula, follow these steps:

Calculate the triangle's semiperimeter s:

s = (a+b+c)/2
Subtract each side from this semiperimeter and multiply each result together:

(s-a)⋅(s-b)⋅(s-c).
Multiply this result by the semiperimeter:

s⋅(s-a)⋅(s-b)⋅(s-c).
Take the square root of this value to get the area of the triangle:

A = √(s⋅(s-a)⋅(s-b)⋅(s-c))
Verify your result with Omni's Heron's formula calculator.

Does Heron's formula always work?

Heron's formula usually works but breaks down for very thin triangles with tiny angles. When one side (c) of a triangle is very small, and the other two sides (a, b) are approximately equal to the semiperimeter s, the values (s-a) and (s-b) will be very small, leading to numerical instability.

In such cases, we can use the following alternative formula for better numerical stability in floating-point arithmetic:

A = ¼⋅√((a+b+c)⋅(-a+b+c)⋅(a-b+c)⋅(a+b-c))

What is the area of a triangle with sides 3, 4, and 5?

The area of a triangle whose sides are 3, 4, and 5 units is 6 sq. units. To find this answer, follow these steps:

Find the semiperimeter s of the triangle:

s = (3+4+5)/2 = 12/2 = 6
Calculate the triangle's area using Heron's formula:

A = √(s⋅(s-a)⋅(s-b)⋅(s-c))
A = √(6⋅(6-3)⋅(6-4)⋅(6-5)) = √(6⋅3⋅2⋅1)
A = √(6⋅6) = 6

Our Heron's formula calculator will help you verify this result.