Slope Calculator

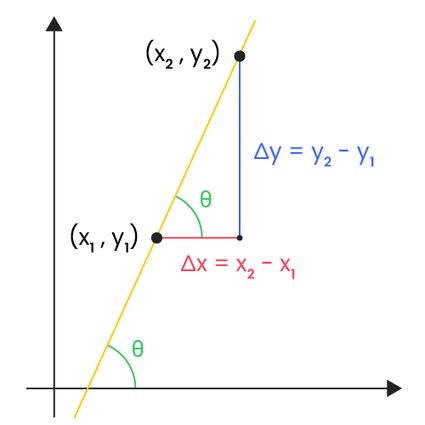
The slope calculator determines the slope or gradient between two points in the Cartesian coordinate system. The slope is basically the amount of slant a line has and can have a positive, negative, zero, or undefined value. Before using the calculator, it is probably worth learning how to find the slope using the slope formula. To find the equation of a line for any given two points that this line passes through, use our slope intercept form calculator.

Here, we will walk you through how to use this calculator, along with an example calculation, to make it simpler for you. To calculate the slope of a line, you need to know any two points on it:

1. Enter the x and y coordinates of the first point on the line.

2. Enter the x and y coordinates of the second point on the line.

3. We instantly get the slope of the line. But the magic doesn't stop there, for you also get a bunch of extra results for good measure:

   • The equation of your function (same as the equation of the line).
   • The y-intercept of the line.
   • The angle the line makes with respect to the x-axis (measure anti-clockwise).
   • Slope as a percentage (percentage grade).
   • The distance between the two points.

For example, say you have a line that passes through the points (1, 5) and (7, 6). Enter the x and y coordinates of the first point, followed by the x and y coordinates of the second one. Instantly, we learn that the line's slope is 0.166667. If we need the line's equation, we also have it now: y = 0.16667x + 4.83333.

You can use this calculator in reverse and find a missing x or y coordinate! For example, consider the line that passes through the point (9, 12) and has a 12% slope. To find the point where the line crosses the y-axis (i.e., x = 0), enter 12% in percent grade (9, 12) as the coordinate of the first point, and x₂ = 0. Right away, the calculator tells us that y₂ = 10.92.

The slope of a line has many significant uses in geometry and calculus. The article below is an excellent introduction to the fundamentals of this topic, and we insist that you give it a read.

Notice that the slope of a line is easily calculated by hand using small, whole number coordinates. The formula becomes increasingly useful as the coordinates take on larger values or decimal values.

It is worth mentioning that any horizontal line has a gradient of zero because a horizontal line has the same y-coordinates. This will result in a zero in the numerator of the slope formula. On the other hand, a vertical line will have an undefined slope since the x-coordinates will always be the same. This will result the division by zero error when using the formula.

1. Identify the coordinates $(x_1, y_1)$ and $(x_2, y_2)$. We will use the formula to calculate the slope of the line passing through the points $(3, 8)$ and $(-2, 10)$.

2. Input the values into the formula. This gives us $(10 - 8)/(-2 - 3)$.

3. Subtract the values in parentheses to get $2/(-5)$.

4. Simplify the fraction to get the slope of $-2/5$.

5. Check your result using the slope calculator.

To find the slope of a line, we need two coordinates on the line. Any two coordinates will suffice. We are basically measuring the amount of change of the y-coordinate, often known as the rise, divided by the change of the x-coordinate, known as the run. The calculations in finding the slope are simple and involve nothing more than basic subtraction and division.

Just as slope can be calculated using the endpoints of a segment, the midpoint can also be calculated. The midpoint is an important concept in geometry, particularly when inscribing a polygon inside another polygon with its vertices touching the midpoint of the sides of the larger polygon. This can be obtained using the midpoint calculator or by simply taking the average of each x-coordinates and the average of the y-coordinates to form a new coordinate.

The slopes of lines are important in determining whether or not a triangle is a right triangle. If any two sides of a triangle have slopes that multiply to equal -1, then the triangle is a right triangle. The computations for this can be done by hand or by using the right triangle calculator. You can also use the distance calculator to compute which side of a triangle is the longest, which helps determine which sides must form a right angle if the triangle is right.

The sign in front of the gradient provided by the slope calculator indicates whether the line is increasing, decreasing, constant or undefined. If the graph of the line moves from lower left to upper right it is increasing and is therefore positive. If it decreases when moving from the upper left to lower right, then the gradient is negative.

The slope calculator is one of the oldest at Omni Calculator, built by our veterans Mateusz and Julia, who make creating accurate scientific tools look easy. The idea for this calculator was born when the two were crunching data analytics and trends and realized how a slope calculator would make their job easier. Even today, you can find them occasionally using this tool for reliable calculations.

We put extra care into the quality of our content so that it is as accurate and dependable as possible. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. You can learn more about our standards in our Editorial Policies page.

The method for finding the slope from an equation will vary depending on the form of the equation in front of you. If the form of the equation is y = mx + c, then the slope (or gradient) is just m. If the equation is not in this form, try to rearrange the equation. To find the gradient of other polynomials, you will need to differentiate the function with respect to x.

1. Use a map to determine the distance between the top and bottom of the hill as the crow flies.

2. Using the same map, or GPS, find the altitude between the top and bottom of the hill. Make sure that the points you measure from are the same as step 1.

3. Convert both measurements into the same units.

4. Divide the difference in altitude by the distance between the two points.

5. This number is the gradient of the hill if it increases linearly. If it does not, repeat the steps but at where there is a noticeable change in slope.

1. Measure the difference between the top and bottom of the slope in relation to both the x and y axis.

2. If you can only measure the change in x, multiply this value by the gradient to find the change in the y axis.

3. Make sure the units for both values are the same.

4. Use the Pythagorean theorem to find the length of the slope. Square both the change in x and the change in y.

5. Add the two values together.

6. Find the square root of the summation.

7. This new value is the length of the slope.

A 1/20 slope is one that rises by 1 unit for every 20 units traversed horizontally. So, for example, a ramp that was 200 ft long and 10 ft tall would have a 1/20 slope. A 1/20 slope is equivalent to a gradient of 1/20 (strangely enough) and forms an angle of 2.86° between itself and the x-axis.

As the slope of a curve changes at each point, you can find the slope of a curve by differentiating the equation with respect to x and, in the resulting equation, substituting x for the point at which you’d like to find the gradient.

The rate of change of a graph is also its slope, which are also the same as gradient. Rate of change can be found by dividing the change in the y (vertical) direction by the change in the x (horizontal) direction, if both numbers are in the same units, of course. Rate of change is particularly useful if you want to predict the future of previous value of something, as, by changing the x variable, the corresponding y value will be present (and vice versa).

Slopes (or gradients) have a number of uses in everyday life. There are some obvious physical examples - every hill has a slope, and the steeper the hill, the greater its gradient. This can be useful if you are looking at a map and want to find the best hill to cycle down. You also probably sleep under a slope, a roof that is. The slope of a roof will change depending on the style and where you live. But, more importantly, if you ever want to know how something changes with time, you will end up plotting a graph with a slope.

A 10% slope is one that rises by 1 unit for every 10 units travelled horizontally (10 %). For example, a roof with a 10% slope that is 20 m across will be 2 m high. This is the same as a gradient of 1/10, and an angle of 5.71° is formed between the line and the x-axis.

To find the area under a slope given by the equation y = mx + c, follow these steps:

1. Define the lower and upper bounds of x to get a value for Δx.
2. Multiply Δx by the slope (m) to obtain Δy.
3. Multiply Δx by Δy.
4. Divide by 2 to give you the area under the slope.

A 1 to 5 slope is one that, for every increase of 5 units horizontally, rises by 1 unit. The number of degrees between a 1 to 5 slope and the x-axis is 11.3°. This can be found by first calculating the slope, by dividing the change in the y direction by the change in the x direction, and then finding the inverse tangent of the slope.