Slope Intercept Form Calculator

The slope intercept form calculator will teach you how to find the equation of a line from any two points that this line passes through. It will help you to find the coefficients of slope and y-intercept, as well as the x-intercept, using the slope intercept formulas. Read on to learn what is the slope intercept form of a linear equation, how to find the equation of a line and the importance of the slope intercept form equation in real life.

Any line on a flat plane can be described mathematically as a relationship between the vertical (y-axis) and horizontal (x-axis) positions of each of the points that contribute to the line. This relation can be written as y = [something with x]. The specific form of [something with x] will determine what kind of line we have. For example, y = x² + x is a parabola, also called a quadratic function. On the other hand, y = mx + b (with m and b representing any real numbers) is the relationship of a straight line.

In this slope intercept calculator, we will focus only on the straight line. You can check our average rate of change calculator to find the relation between the variables of non-linear functions.

Linear equations, or straight-line equations, can be quickly recognized as they have no terms with exponents in them. (For example, you will find an x or a y, but never an x².) Each linear equation describes a straight line, which can be expressed using the slope intercept form equation.

As we have seen before, you can write the equation of any line in the form of y = mx + b. This is the so-called slope intercept form because it gives you two important pieces of information: the slope m and the y-intercept b of the line. You can use these values for linear interpolation later.

The term slope is the incline, or gradient, of a line. It tells us how much y changes for a fixed change in x. If it is positive, the values of y increase when x increases. If it is negative, y decreases with an increasing x. You can read more about it in the description of our slope calculator.

The y-intercept is the value of y at which the line crosses the y-axis. To find it, you have to substitute x = 0 in the linear equation. You will see later why the y-intercept is an important parameter in linear equations, and you will also learn about the physical meaning of its value in certain real-world examples.

Still need to know how to find the slope intercept form of a linear equation? We will assume you know two points that the straight line goes through. The first one will have coordinates (x₁, y₁) and the second one (x₂, y₂). Your unknowns are the slope m and the y-intercept b.

Firstly, substitute the coordinates of the two points into the slope intercept equation:

(1) y₁ = mx₁ + b

(2) y₂ = mx₂ + b

Then, subtract the first equation from the second:

y₂ - y₁ = m(x₂ - x₁)

Finally, divide both sides of the equation by (x₂ - x₁) to find the slope:

m = (y₂ - y₁)/(x₂ - x₁)

Once you have found the slope, you can substitute it into the first or second equation to find the y-intercept:

y₁ = x₁(y₂ - y₁)/(x₂ - x₁) + b

b = y₁ - x₁(y₂ - y₁)/(x₂ - x₁)

This slope intercept form calculator allows you to find the equation of a line in the slope intercept form. All you have to do is give two points that the line goes through. You need to follow the procedure outlined below.

1. Write down the coordinates of the first point. Let's assume it is a point with x₁ = 1 and y₁ = 1.

2. Write down the coordinates of the second point as well. Let's take a point with x₂ = 2 and y₂ = 3.

3. Use the slope intercept formula to find the slope:

   m = (y₂ - y₁)/(x₂ - x₁) = (3-1)/(2-1) = 2/1 = 2.

4. Calculate the y-intercept. You can also use x₂ and y₂ instead of x₁ and y₁ here.

   b = y₁ - m × x₁ = 1 - 2×1 = -1

5. Put all these values together to construct the slope intercept form of a linear equation:

   y = 2x - 1.

6. You can also use the distance calculator to find the distance between two points.

It is also always possible to find the x-intercept of a line. It is the value of x at which the straight line crosses the x-axis (it means the value of x for which y equals 0). You can calculate it in the following way:

0 = mx + b

x = -b/m

As we can see, the only condition that must be met is that coefficient m is different from zero.

Our slope intercept form calculator will display both the values of the x-intercept and y-intercept for you. Still, if you would like to learn more about them, we recommend you visit our x- and y-intercept calculator.

We have already seen what is the slope intercept form, but to understand why the slope intercept form equation is so useful, you should know some applications it has in the real world. Let's see a couple of examples. We will start with simple ones from physics so that you can get an intuitive idea of what the y-intercept and x-intercept mean.

Imagine a car moving at a fixed speed toward you. Its movement can be plotted as time versus the distance the car is from you (as shown above). This means that the x-axis will represent the time passed, and the y-axis will represent the distance to the car. You can even imagine the car has started to move before you started the timer (that is: before t = 0).

Now, if you look at the y-intercept (x = 0), the point at which you started to keep track of time is t = 0. And so, the value of y at this point will indicate the starting position (distance) of the car with respect to you. This value is, as we have discussed before, the same as the value of b in the slope intercept form of a straight-line equation.

Looking now at the x-intercept (y = 0), this will be the point at which the distance from the car to you will be 0. Then the value of x at this point will be the time when you and the car were at the same place. Let's hope that means you were inside the car and not under.

The car example above is a very simple one that should help you understand why the slope intercept form is important and, more specifically, the meaning of the intercepts. In this article, we will mostly talk about straight lines, but the intercept points can be calculated for any kind of curve (if it crosses an axis).

In fact, the example above does not fit a linear equation and still has both intercepts. The same is true for any other parabola or another shape.

One equation that is guaranteed to have a y-intercept but not necessarily an x-intercept is a parabola. This is equation is shown in the image above. It has a maximum or a minimum (depending on the orientation). If this maximum is below the x-axis or the minimum is above the x-axis, there will never be an x-intercept.

However, unlike humans, not all equations are equal. Some of the formulas describe curves that might never intercept the x-axis, the y-axis, or both. Let's see in a bit more detail how this can be.

We can distinguish 3 groups of equations depending on whether they have a y-intercept only, an x-intercept only, or neither. The first group (y-intercept only) can have almost any type of equation, including linear equations. A good easy example is y = 3 (or any other constant value of y except for 0) since this is a line parallel to the x-axis and will, thus, never cross or intercept it. Please don't try to calculate these types of intercepts on this slope intercept form calculator as these types of equations can potentially break the Internet.

The second and third groups of equations are a bit more tricky to imagine and to understand them well, we need to introduce the concept of an asymptote. An asymptote is a line (that can be expressed as a linear equation) to which the function or curve we are talking about gets closer and closer but never actually crosses or touches that line.

The definition might not seem totally clear, but if we look at an example equation, we will have fewer problems with understanding it. Let's take the equation y = 1/x. If we try to find the y-intercept by substituting x = 0, we arrive at what is called a mathematically undefined expression since it makes no sense to divide by 0.

If we take values closer and closer to 0 (something like 0.1, then 0.001, 0.000001...), we can see that the value of y increases very rapidly. So around the point x = 0, we know that y would have a massive value, but because of how math works, it does not have a defined value for that exact point. Sometimes people may say 1/0 = ∞, but the reality is that infinity is not a number but a concept.

In this case, the linear equation x = 0 represents the asymptote of the function y = 1/x, which means that y = 1/x will never intercept that line and, thus, will not have a y-intercept. In general, any time that a function has an asymptote that lies on one of the axes, it will be missing at least one of the intercepting points.

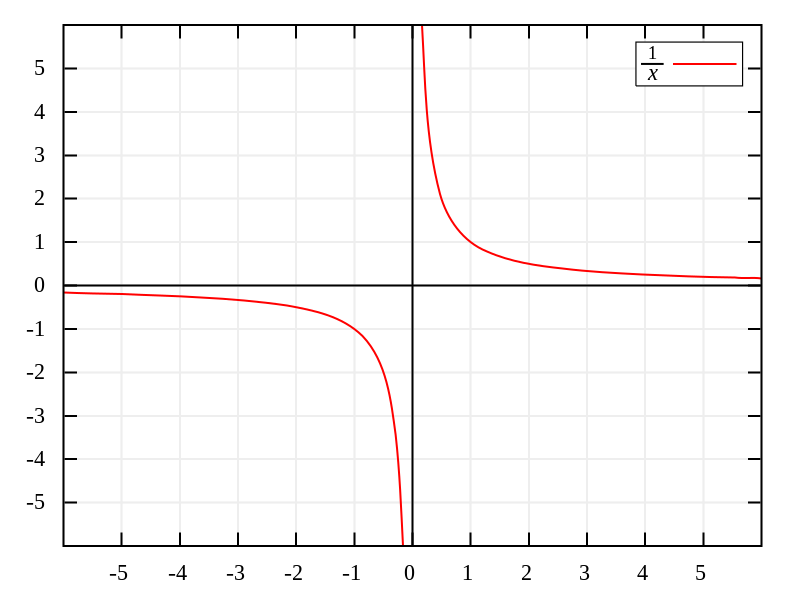
In fact, the example we have shown you (y = 1/x) also has an asymptote for y = 0, i.e., the x-axis. For the same reason as before, y = 0 is never achievable by the formula because it would require x = ∞, and as we said before, it is impossible to achieve that since infinity is a concept and not a number.

Before we move to our next topic, it is important to note that we have made extreme over-simplifications when talking about infinity, but we feel it is a good and fast approach for those that are not used to the concept of working with infinity in math. We recommend that you learn more about the proper ways of infinity, starting with the undefined expressions in math.

One could easily think that the usefulness of linear equations is very limited due to their simplicity. However, the reality is a bit different. Linear equations are at the core of some of the most powerful methods to solve minimization and optimization problems.

Minimization problems are a type of problem in which one would like to find how to make one of the variables as small as possible. This variable could be, for example, the difference between a prediction made by a model and reality. These types of problems are one of the most common problems and are at the core of machine learning and scientific experiments.

One of the most common and powerful methods to find the minimum value of an equation or formula is the so-called Newton method, named after the genius that invented it. The way it works is by using derivatives, linear equations, and x-intercepts:

This method consists of choosing a value of x for the equation and calculating the derivative of the equation at that point. Using the derivative as the slope of a linear equation that passes through that exact (x, y) point, the x-intercept is then calculated. This is one of the situations in which the slope intercept form comes in handy.

Once the x-intercept is calculated, that value of x is used to repeat the process above, a specific number of times, until we arrive at a value of y that is minimum (which means that the derivative will be 0). In real life, arriving at the exact minimal point is not possible to do in a finite amount of time, so typically, people will settle for a "close enough" value.

One very common example is when using the least squares method to fit some data to a formula or trend. In this case, the value that we want to minimize is the sum of the squared distance from the trend line to the data points, where the distance is calculated along a perpendicular line from the point to the trend line.

No, standard form, and slope-intercept form are two different ways of describing a line:

• Slope intercept form reads y = mx + b, where m is the slope (steepness) of the line, and b is the y-intercept, i.e., the value at which the line intersects the vertical axis. For example, y = -2x + 3.
• Standard form reads Ax + By + C = 0, where A, B, C are integers. For example, 2x + y - 3 = 0.

If you want to rewrite your standard form equation to the slope-intercept form, follow these steps:

1. Write down the standard form of your line: Ax + By + C = 0.
2. Move Ax and C on the right-hand side so that By remains by itself on the left side: By = -Ax - C.
3. Divide both sides by B: y = -(A/B)x - (C/B).
4. As you can see, we've got the slope intercept form y = mx + b with slope m = -A/B and intercept b = -C/B.

The slope (aka gradient) describes the steepness of a line. Slope can be
positive, negative, or zero and:

• Positive slope means the line rises from left to right.
• Negative slope means the line goes downwards from left to right.
• Zero gradient means the line is horizontal.

The bigger the absolute value of the gradient, the faster the line increases/decreases. In fact, the value of the slope is exactly the amount by which the line increases/decreases when x increases by one unit.

The slope is m = 1. To get this result, use the formula ‘m = tan(α)’, where α is the angle between the line and the x-axis. Since tan(45°) = 1, we get the slope 1, as claimed.