y Intercept Calculator
This y-intercept calculator is the perfect tool to calculate the x- and y-intercept of any given line. Additionally, you can use it to find the line equation from its slope and the x- or y-intercept.
Finding intercepts of straight lines is a simple process, but it is pretty common to get the basics mixed up. Let's discuss the following basics in this article so that you're always ready:
- How do you find the y-intercept of any line?
- How do you find the x-intercept of any line?
- How do you find the line equation from its intercepts?
If you're interested in finding the line equation in different forms, we recommend our popular slope intercept form calculator and point slope form calculator.
Slope, intercepts, and the general line equation
We can express the most general form of a straight line in 2-dimensional space as:
where:
- is the coefficient of the term;
- is the coefficient of the term;
- is the constant term; and
- and are the variables representing the two dimensions.
You can plot this line on a graph sheet if you know at least two points that lie on this line. We define the y-intercept of this line as the point at which it crosses (or intersects) the y-axis. Specifically, it refers to the y-coordinate of this point, although it is also common to call the point itself the y-intercept.
Similarly, the line's x-intercept would be the point (or the x-coordinate) where it intersects the x-axis.
The slope (or gradient) of a line is the amount of change in for a change in . You can learn more about the slope of a line using our slope calculator.
We can express the slope, y-intercept and x-intercept of any line using these equations:
where:
- is the y-intercept of the line;
- is the x-intercept of the line; and
- is the slope of the line.
In the following sections, we'll prove these equations with an example — but first, let's discuss another form of a line equation.
You can read more about slopes and y-intercepts in our guide, Slope and Y-intercept Formula
Slope-intercept form
We can also express a line equation in terms of its slope and y-intercept:
where:
- is the line's slope; and
- is the line's y-intercept, i.e. .
We could rewrite it to include the y-intercept from the start:
You'll find this form very useful when formulating most line equations if you can calculate the slope and y-intercept beforehand.
How do you find the y-intercept of a line?
To find the y-intercept of a line given by ax + by + c = 0, follow these simple steps:
- Substitute the value x = 0 into the line equation to get by + c = 0.
- Rearrange this equation to find the y-intercept yc, as yc = −c/b.
- Verify your results using our y-intercept calculator.
Or, if the line equation is in the slope-intercept form y = mx + c, you can directly extract the term c as the line's y-intercept yc.
For example, consider a line given by the equation . The y-intercept lies on the intersection of the y-axis (the line defined by ) and our line . So, we insert in to obtain:
How do you find the x-intercept of a line?
To find the x-intercept of a line given by ax + by + c = 0, follow these simple steps:
- Substitute the value x = 0 into the line equation to get ax + c =0.
- Rearrange this equation to find the y-intercept xc, as xc = −c/a.
- Verify your results using our y-intercept calculator.
These steps are applicable even if the line equation is in slope-intercept form: y = mx + c, giving you xc = −c/m.
Again, consider the line . Its x-intercept lies on the intersection point of the x-axis () and . So, we insert in to obtain:
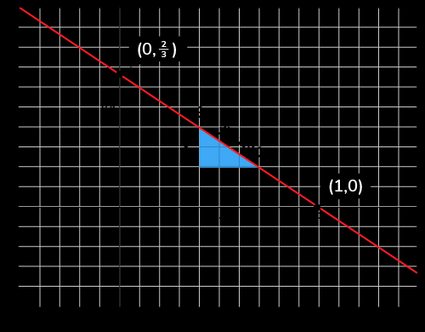
How do you find the line equation from its intercepts?
To find the line equation from its x-intercept (xc, 0) and y-intercept (0, yc), follow these steps:
- Determine the slope m of the line using m = (0 − yc)/(xc − 0) to get m = −yc/xc.
- Formulate the line equation in the slope-intercept form y = mx + c, keeping in mind that c = yc.
- Simplify and rearrange as required, or use the equation as it is.
Once again, let's consider the line with x-intercept and y-intercept. Can we find the line equation with just these intercepts? Let's find out.
- We can determine the slope of this line using these two intercept points and :
- Formulate the line equation in the slope-intercept form :
- Simplify this equation and rearrange it to get .
How to calculate x- and y-intercepts using this y-intercept calculator
You can use this y-intercept calculator in three modes:
-
To calculate the x- and y-intercepts along with the line's slope from its general equation:
- Choose the mode "Line equation is
ax + by + c = 0". - Enter the values for
a,b, andc, and the calculator will provide you with all the answers!
- Choose the mode "Line equation is
-
To calculate the slope, y-intercept, and x-intercept of a line from its slope-intercept form:
- Choose the mode "Line equation is
y = mx + c". - Enter the values for
mandc. - Sit back and relax as the calculator takes care of the rest.
- Choose the mode "Line equation is
-
To find an equation with the intercepts given, use the mode "Line equation is to be determined."
- Enter the values of
x-interceptandy-intercept. - Enjoy the fast and accurate results.
- Enter the values of
Our calculator will also present you with a summary of results and a helpful graph in all these modes!
Pat yourself on your back for learning something new today! We believe you're ready to explain to others how to find the slope, y-intercept, and x-intercept of a line.
FAQs
What is the y-intercept of the line 2x + 3y = -9?
−3 is the y-intercept of the line 2x + 3y = −9. To find this yourself, follow these steps:
- Substitute
x = 0into the line's equation to get2×0 + 3y = −9, or3y = −9. - Divide both sides by
3to gety = −3. - Verify your results using our y-intercept calculator.
Do all straight lines have a y-intercept?
No. Some lines run parallel to the y-axis, and thus don't have a y-intercept. However, every line in two dimensions has at least one intercept, be it x- or y-intercept.