Point Slope Form Calculator

Q: How do I calculate the intercept given point-slope form?

The y-intercept of a line with point-slope form y - b = m(x - a) is given by the formula intercept = b - ma . For instance, for the line y - 1 = 2(x - 3) you get the intercept 1 - 6 = -5 .

Q: What is the point slope formula with zero slope?

If the slope is zero, the point-slope formula reduces to y - b = 0 . This equation describes a horizontal line that crosses the vertical axis at y = b .

Q: Can point-slope form be the same as the slope intercept form?

Yes! Take the line with slope intercept form y = mx + b . Let us write down its point-slope form for the point (0, b) . We get y - b = m(x - 0) , which is the same (up to the trivial transformation of moving b to the right-hand side) as the slope-intercept form.

The point-slope form calculator will show you how to find the equation of a line from a point on that line and the line's slope. Soon, you will know what is point-slope form equation, and learn how is it different from the slope-intercept form equation. We also came up with two exercises, and we'll explain how to solve them in the last paragraph.

Let's start with the basics and discuss what the slope is.

What is a slope?

The slope, also known as the gradient, is the marker of a line's steepness. If it's positive, it means the line rises. If it's negative – the line decreases. If it's equal to zero, the line is horizontal.

You can find the slope between two points by estimating rise over run – the difference in height over a distance between two points.

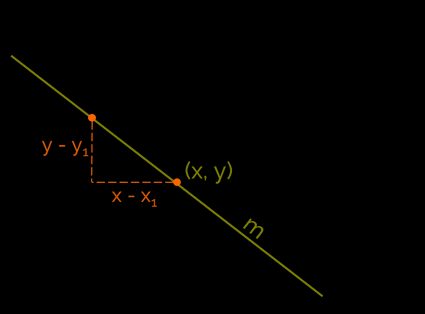
point-slope form and slope-intercept form of a straight line equation

So, the slope formula is:

m = change in y / change in x = (y – y₁) / (x – x₁)

The point-slope form equation is a rearranged slope equation.

To find the gradient of non-linear functions, you can use the average rate of change calculator.

🙋 For more information go to the slope calculator.

What is the point-slope form?

There is more than one way to form an equation of a straight line. Point-slope form is a form of a linear equation, where there are three characteristic numbers – two coordinates of a point on the line, and the slope of the line. The point slope form equation is:

\small y - y_1 = m \cdot (x - x_1),

where:

$\small x_1, y_1$ are the coordinates of a point, and
$\small m$ is the slope.

Do you see the similarity to the slope formula? What you might not know is that it's not the only way to form a line equation. The more popular is the slope intercept form:

\small y = m \cdot x + b,

where:

$\small m$ is the slope; and
$\small b$ is the intercept of the y-axis.

The truth is that this is nothing else than a more precise point-slope form. A straight line intercepts the y-axis in a point (0, b). If you choose this point – (0, b), as a point that you want to use in the point-slope form of the equation, you will get:

$\small y - b = m \cdot (x - 0)$ , which is the same as $\small y = m \cdot x + b$ .

In the two graphs below, you can see the same function, only described with two different forms of a linear equation:

To learn how to find the x-intercept and y-intercept of a line, visit our x- and y-intercept calculator.

How to find the equation of a line with slope and coordinates of a point?

Let's have a look at two exercises, to understand the topic more clearly.

The slope of a line is 2. It passes through point A(2, -3). What is the general equation of the line?

Identify the point coordinates:
- x₁ = 2,
- y₁ = -3.
Identify the slope:
- m = 2
Input the values into the point-slope form formula:
- $\small y - y_1 = m (x - x_1)$
- $\small y - (-3) = 2(x - 2)$
Simplify to get the general equation:
- $\small y = 2x - 4 -3$
- $\small 0 = 2x - y - 7$
And you have the answer. Now, you can check your result with our point-slope form calculator.

Let's solve an exercise with a more relatable subject.

Let's say you got a puppy. When you got him, he was 14 pounds. It grew 0.2 pounds every day, and after 30 days, he was 20 pounds. Find the general equation of the puppy's growth.

The slope is the change of weight per day: m = 0.2
The characteristic point is 20 pounds on 30th day: (x₁, y₁) = (30, 20)
Now, input the values into the point-slope formula:

$\small y - 20 = 0.2 \times (x - 30)$
Simplify the equation to get the general equation:

$\small 0 = 0.2x - y + 14$

💡 If you need to find a different point on your line, click on the Input one coordinate and get the other button. Then, enter one coordinate, and get the other.

And here you have it! We hope you enjoyed our point-slope form calculator!

FAQs

How do I convert point-slope to slope intercept?

If you are given a point-slope form of a line, you can get the slope intercept by following these steps:

Write down your point-slope form:

y - b = m(x - a)
Expand the right-hand side:

y - b = mx - ma
Add b to both sides:

y = mx - ma + b.
This is slope-intercept form! The slope is m, and the intercept is -ma + b.

How do I calculate the intercept given point-slope form?

The y-intercept of a line with point-slope form y - b = m(x - a) is given by the formula intercept = b - ma. For instance, for the line y - 1 = 2(x - 3) you get the intercept 1 - 6 = -5.

What is the point slope formula with zero slope?

If the slope is zero, the point-slope formula reduces to y - b = 0. This equation describes a horizontal line that crosses the vertical axis at y = b.

Can point-slope form be the same as the slope intercept form?

Yes! Take the line with slope intercept form y = mx + b. Let us write down its point-slope form for the point (0, b). We get y - b = m(x - 0), which is the same (up to the trivial transformation of moving b to the right-hand side) as the slope-intercept form.