Average Rate of Change Calculator
Table of contents
What is rate of change? – the average rate of change definitionAverage rate of change formulaHow to find the average rate of change? – first exampleHow to find the average rate of change? - second exampleFAQsThe average rate of change calculator is here to help you understand the simple concept hidden behind a long, little bit confusing name. What is the rate of change? Generally speaking, it shows the relationship between two factors. Look for a more precise average rate of change definition below. We will also demonstrate and explain the average rate of change formula with a couple of examples of how to use it.
Prefer watching over reading? Learn all you need in 90 seconds with this video we made for you:
What is rate of change? – the average rate of change definition
Everything keeps moving. Change is inevitable. Starting with the acceleration of your bike or car, through to population growth, from the blood flow in your veins to the symbiosis of your cells, the rate of change allows us to establish the value associated with those changes.
The average rate of change is a rate that describes how one number changes, on average, in relation to another. If you have a function, it is the slope of the line drawn between two points. But don't confuse it with slope. You can use the average rate of change for any given function, not only linear ones.
🙋 If you want to learn more about slope go to the slope calculator.
Average rate of change formula
In the following picture, we marked two points to help you better understand how to find the average rate of change.
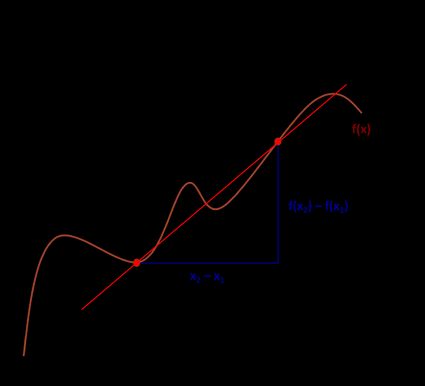
The average rate of change formula is:
A = [f(x₂) − f(x₁)] / [x₂ − x₁]
where:
- (x₁, f(x₁)) – Coordinates of the first point; and
- (x₂, f(x₂)) – Coordinates of the second point.
If it's positive, it means that one coordinate increases as the other also increases. For example, the more you ride a bike, the more calories you burn.
It's equal to zero when one coordinate changes but the other one does not. A good example might be not studying for your exams. As time starts running out, the amount of things to learn doesn't change.
The average rate of change is negative when one coordinate increases while the other one decreases. Let's say you're going on a vacation. The more time you spend on your travel, the closer you are to your destination.
💡 You can learn other ways to describe the difference between two points in the rise over run calculator.
How to find the average rate of change? – first example
Let's calculate the average rate of change of distance (average speed) of a train going from Paris to Rome (1420.6 km). On the following chart, you can see the change in distance over time:
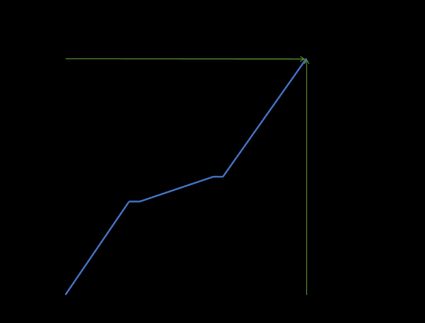
As you see, the speed wasn't constant. The train stopped two times, and in between stops, it went significantly slower. But for calculating the average speed, the only variables that matter are the change in distance and the change in time. So, if the coordinates of the first point are (0, 0), and the coordinates of the second point are the distance between two cities, and the time of travel is (1420.6, 12.5), then:
A = (1420.6 - 0) / (12.5 - 0) = 113.648 [km/h]
On average, the train was going 113.648 kilometers per hour. Now, let's look at a more mathematical example.
How to find the average rate of change? - second example
You have been given a function:
f(x) = x² + 5x − 7
Find the average rate of change over the interval [-4, 6].
-
Find values of your function for both points:
f(x₁) = f(-4) = (-4)² + 5 × (-4) − 7 = -11
f(x₂) = f(6) = 6² + 5 × 6 − 7 = 59
-
Use the average rate of change equation:
A = [f(x₂) − f(x₁)] / [x₂ − x₁] = [f(6) − f(-4)] / [6 − (-4)] = [59 − (-11)] / [6 − (-4)] = 70 / 10 = 7
If you enjoyed the average rate of change calculator, feel free to check out our other tools like this distance calculator, where you can find the distance between points or lines.
Is average rate of change the same as slope?
Not precisely. The average rate of change reflects how a function changes on average between two points. On the other hand, we define the slope of a function as the slope of the line tangent to the curve at a specific point. In a linear function, every point changes identically, so the average rate of change and slope are equal.
How do you find the average rate of change of a function?
To find the average rate of change of a function, follow these steps:
-
Get the (x, y) coordinates of the starting point. We'll call these (x₀, y₀).
-
Get the (x, y) coordinates of the endpoint. These will be (x₁, y₁).
-
Replace both within the average rate of change (A) formula:
A = (y₁ − y₀)/(x₁ − x₀).
What is the average rate of change of y = 2x?
The average rate of change of y = 2x is 2. Since it is a linear function, the average rate of change is just the function's slope. In this case, for every change in the x-coordinate, the y-coordinate will double it.
Is speed an example of average rate of change?
If the speed is constant, yes. Speed reflects how the position changes instantaneously with respect to time. So, if an object were moving at a constant speed, the average rate of change in the position would tell us at which speed it is traveling.