Sine Calculator

With this sin calculator, you can find the sin value in the blink of an eye - all you need to do is typing the angle in degrees or radians. The calculator also works the other way round - put the value of sine into the proper box, and we'll calculate the angle for you - isn't that awesome? As a result, you'll get the angle from the $<-90\degree, 90\degree>$ range. Scroll down to understand what is a sine and to find the sine definition, as well as simple examples and the sine graph. Also, you'll find there a simple table with values of sine for basic angles, such as $\sin(0)$, $\sin(30\degree)$ and many more.

Prefer watching over reading? Learn all you need in 90 seconds with this video we made for you:

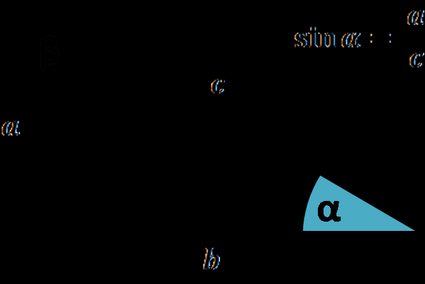
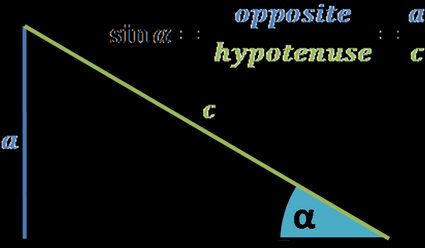
Sine is one of the three most common (others are cosine and tangent, as well as secant, cosecant and cotangent). The abbreviation of sine is sin e.g. $\sin(30\degree)$. Most common and well known sine definition is based on right-angled triangle. Let's start with nomenclature of triangle sides which will be useful in further steps. As the picture on the right shows, we can name the sides of a right triangle as:

• Adjacent side - the shorter adjacent side of the angle of interest (in this case, angle $\alpha$). This side is adjacent to both the angle of interest and the right angle.
• Opposite side - merely the side opposite to the angle of interest.
• Hypotenuse - the opposite side to the right angle, it's always the longest side in the right triangle.

So if our angle of interest change to $\beta$, then the adjacent and opposite side will be exchanged - but a hypotenuse stays the same. Did you expect to find right triangles here? Trigonometry and triangles share many characteristics: we calculate Pythagorean theorem more often when studying angles than triangles!

1. Right-angled triangle definition

The sine of an angle is the length of the opposite side divided by the length of the hypotenuse

with the assumption that the angle is acute ($0\degree < \alpha < 90\degree$ or $0 < \alpha < \pi/2$).

The other sine definition is based on the unit circle.

2. Unit circle

In this definition, α is any angle, and sine is a y-coordinate of the point of intersection between a unit circle and a line from the origin, making an angle of α. Sounds complicated, but if you look at the picture, everything should be clear. For a unit circle, the radius is - of course - equal to $1$, so the sine is:

Look at the picture again - do you understand now where does the Pythagorean trigonometric identity come from?

Other important properties of a sine function:

• Range of sine is $-1 \leq \sin(\alpha) \leq 1$
• Sine period is equal to $2\pi$
• It's an odd function, which means that $\sin(-\alpha) = -\sin(\alpha)$
• Roots of the sine function: $k\pi$

This is just one of our trigonometric functions calculators: discover the others at the cosine calculator and tangent calculator!

The basic equation of a sine wave - sinusoid - may be expressed as:

Or:

where:

• $A$ — The amplitude
• $f$ — The ordinary frequency - the number of oscillations that occur each second of time
• $\omega = 2\pi f$ — The angular frequency, in units of radians per second
• $\varphi$ — The phase, specifies (in radians) where in its cycle the oscillation is at $t = 0$.

Did you noticed that the graphs of the sine and cosine functions are sinusoids of different phases?

Sine waves are very useful and find applications in many different fields, such as mathematics, physics, engineering or signal processing. But sinusoids are present all around us! Let's take for example wind, sound, or light waves - all these are the exemplary sine waves occurring in nature.

The sine graph below shows the sinusoid in $<-2\pi, 2\pi>$ range:

Exact sine value is particularly easy to remember and to define for certain angles:

Also, you can observe how the sine function behaves according to a quadrant. For angles out of the range of this table, remember about periodicity of the sine $\sin(\alpha + 360\degree) = \sin(\alpha)$.

It couldn't be easier! Just:

1. Type the angle into the proper box. You can choose between two units - degrees and radians. Let's assume we want to find the sine of $40\degree$.
2. The sin calculator shows the result immediately! It's equal to $0.6428$ (don't forget that's only an approximate value, as the exact one can be calculated for specific angles only).

You can use the calculator the other way round as well:

1. Enter the sin value. For example, let's type $0.7$.
2. Here we go! The sine calculator finds the angle as well! It's $44.43\degree$. Remember that we show the angle in a $<-90\degree, 90\degree>$ range - but a sine function is periodic, you can easily find other angles for which the same sine value occurs, just add or subtract multiples of $360\degree$ ($2\pi$) e.g.$0.7 = sin(44.43\degree) = sin(404.43\degree) = sin(-315.57\degree) = ...$. Don't forget about the parity - the function is odd, so$\sin(-\alpha) = -\sin(\alpha)$$.

Now, as you understand what a sine is, check out more advanced application of that function: visit our law of sines calculator to meet the sine in its most common usage, solving triangle problems.