Trigonometry Calculator

This trigonometry calculator will help you in two popular cases when trigonometry is needed. If you want to find the values of sine, cosine, tangent, and their reciprocal functions, use the first part of the calculator. Are you searching for the missing side or angle in a right triangle using trigonometry? Our tool is also a safe bet! Type 2-3 given values in the second part of the calculator, and you'll find the answer in a blink of an eye. Scroll down if you want to learn about trigonometry and where you can apply it.

There are many other useful tools when dealing with trigonometry problems. Check out two popular trigonometric laws with the law of sines calculator and our law of cosines calculator, which will help you to solve any kind of triangle.

This trigonometry calculator has two sections that perform two different functions using trigonometry. The following instructions should help you work your way around this calculator with ease:

1. The first section takes an angle input and gives you a list of trigonometric function values for this angle. To input in a different unit, click on the unit to change it, and then enter the angle.

For example, to find the value of sin(45°), we merely enter 45 degrees as the angle. The calculator instantly tells you that sin(45°) = 0.70710678. It also gives the values of other trig functions, such as cos(45°) and tan(45°).

2. The second section uses trigonometry to determine the missing parameters of a right-angled triangle:

   1. First, select what parameters are known about the triangle. You can choose between "two sides", "an angle and one side", and "area and one side".

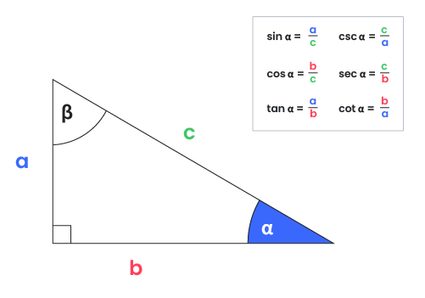
   2. Refer to the diagram at the bottom of the calculator to understand the parameter labels. Enter the parameters based on your choice. If you need to input a parameter in a different unit, change the unit before entering a value.

   3. The tool will calculate the missing parameters using trigonometry.

For example, if we know two sides, a = 7 cm and b = 12 cm, we enter them in this calculator. Right away, we see that c = 13.892 cm, α = 30.256°, and β = 59.74°.

We can use this section in reverse, too! Say we know the angle β = 30°, b = 10 in, and c = 20 in. First, enter β = 30°, and instantly we learn that α = 60°. Now, enter b = 10 in (ensuring the unit is inches first). Similarly, input c = 20 in, and we see that a = 17.32 in.

If you're wondering how trigonometry can help you learn so much about triangles, continue reading this article. It answers many questions that people new to trigonometry should know.

Trigonometry is a branch of mathematics. The word itself comes from the Greek trigōnon (which means "triangle") and metron ("measure"). As the name suggests, trigonometry deals primarily with angles and triangles; in particular, it defines and uses the relationships and ratios between angles and sides in triangles. The primary application is thus solving triangles, precisely right triangles, and any other type of triangle you like.

Trigonometry has plenty of applications: from everyday life problems such as calculating the height or distance between objects to the satellite navigation system, astronomy, and geography. Also, sine and cosine functions are fundamental for describing periodic phenomena - thanks to them, we can describe oscillatory movements (as in our simple pendulum calculator) and waves like sound, vibration, or light.

Many fields of science and engineering use trigonometry and trigonometric functions, namely: music, acoustics, electronics, medicine and medical imaging, biology, chemistry, meteorology, electrical, mechanical, civil engineering, and even economics... The trigonometric functions are really all around us!

To find the missing sides or angles of the right triangle, all you need to do is enter the known variables into the trigonometry calculator. You need only two given values in the case of:

• one side and one angle
• two sides
• area and one side

Remember that if you know two angles, it's not enough to find the sides of the triangle. Two triangles having the same shape (which means they have equal angles) may be of different sizes (not the same side length) - that kind of relationship is called triangle similarity. If the sides have the same length, then the triangles are congruent.

Hi, I'm Hanna, the brainchild of this trigonometry calculator, and I'm a doctor of mechanical engineering and a maestro at creating scientific tools. I knew a good trigonometry calculator would help me get the right depth of field for my photography, so I sat down to create it. Thanks to this, I have captured some crisp photos of colorful birds in the wild!

We put extra care into the quality of our content so that they are as accurate and reliable as possible. Each tool is peer-reviewed by a trained expert and then proofread by a native speaker. To learn more about our standards, please check the Editorial Policies page.