Dot Product Calculator
The vector dot product calculator comes in handy when you are solving vector multiplication problems. Instead of calculating the scalar product by hand, you can simply input the components of two vectors into this tool and let it do the math for you.
Please keep reading to learn the dot product formula our calculator uses, how to estimate the dot product of two vectors, and how to generalize the formula for the matrix dot product. Together with the cross product calculator, you'll learn that vector algebra isn't anything to worry about!
Vector multiplication types
There are two main types of vector multiplication: the dot product (also called the scalar product), denoted with the symbol "·", and the cross product (also known as the vector product), indicated with the symbol "×". The main difference is that the product of the dot operation is a single number, while the outcome of the cross operation is a vector.
What is the dot product formula?
Let's assume that we will perform all our calculations in 3D space. That means that every vector can be written down using three components:
- a = [a₁, a₂, a₃]
- b = [b₁, b₂, b₃]
Geometrically, the dot product is described as the product of the vectors' magnitudes multiplied by the cosine of the angle between them. We can express this using the equation:
- a⋅b = |a| × |b| × cos α
If you are not sure what the magnitude of a vector is or how to calculate it, head to the unit vector calculator for more details on the subject.
You can probably notice that if the angle between two vectors is equal to 90°, then the scalar product will always be equal to 0, regardless of the vectors' magnitudes. Similarly, if the angle is equal to 0° (the vectors are collinear), the dot product is found by multiplying the multitudes only. In other words, the bigger the relative slope between two vectors, the higher the dot product value. You can calculate the slope of a vector using the slope calculator.
Algebraically, the dot product is the sum of the products of the vectors' components. For three-component vectors, the dot product formula looks as follows:
a⋅b = a₁ b₁ + a₂ b₂ + a₃ b₃
In a space that has more than three dimensions, you simply need to add more terms to the summation. If, on the other hand, you want to multiply vectors in a 2D space, you have to omit the third term of the formula.
The dot product calculator can also work as a tool to find the angle between two vectors for which cosine is the ratio between the scalar product and the vectors' magnitudes:
cos α = a⋅b / (|a| × |b|)
To learn more about ratios such as this one, check out our ratio calculator.
Determining the vector dot product
So, how does our vector multiplication calculator work? Follow this step-by-step example to get a better understanding of the principle behind this process.
-
Choose your vector a. For example, we will take a = [4, 5, -3].
-
Choose your vector b. Let's assume it is equal to b = [1, -2, -2].
-
Calculate the product of the first component of each vector. In this case, it is equal to
4 × 1 = 4. -
Calculate the product of the second (middle) component of each vector. In this case, it is equal to
5 × (-2) = -10. -
Calculate the product of the third component of each vector. In this case, it is equal to
(-3) × (-2) = 6. -
Add all of these results together to find the dot product of the vectors a and b.
4 + (-10) + 6 = 0
The result is 0. This outcome is the scalar product of these two vectors. This means that they are perpendicular to each other (the angle between them is equal to 90°).
Scalar product in spherical coordinates
It is also possible to calculate the scalar product of two vectors if they are written in spherical coordinates. To deal with the challenge, we need to express our new coordinates with the radius r and two angles θ, φ:
- x₁ = r₁ × sin φ₁ × cos θ₁;
- y₁ = r₁ × sin φ₁ × sin θ₁; and
- z₁ = r₁ × cos φ₁.
And analogically for x₂, y₂, z₂. Then, the result will be:
a⋅b = x₁ × x₂ + y₁ × y₂ + z₁ × z₂ = r₁ × r₂ × sin φ₁ × cos θ₁ × sin φ₂ × cos θ₂ + r₁ × r₂ × sin φ₁ × sin θ₁ × sin φ₂ × sin θ₂ + r₁ × r₂ × cos φ₁ × cos φ₂.
If we use the equation for the cosine of the angles difference, the formula simplifies to:
a⋅b = r₁ × r₂ × (sin φ₁ × sin φ₂ × cos(θ₁-θ₂) + cos φ₁ × cos φ₂).
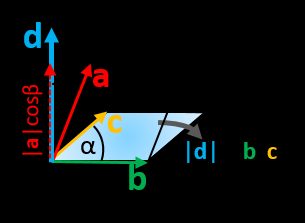
Matrix dot product
Actually, the dot product operation can not only be done for vectors but also for more general cases – matrices. As a result, we obtain another matrix, C, such that:
It's analogous to the scalar product of simple vectors, but the procedure has to be repeated several times for each element.
However, not every two matrices can be multiplied. If we consider A as m × n and B as k × l matrices, then the matrix product C = A⋅B is well-defined only when n = k. Similarly, the matrix product D = B⋅A exists only if l = m. In other words, the number of columns of the left matrix has to match the number of rows in the second one. Note that if at least one of the matrices A, B is not square, then at most one of the two products A⋅B, C⋅D can be defined (and, in many cases, none of them can).
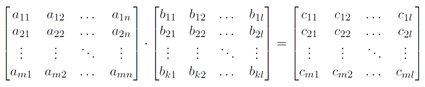
As you may have already noticed, products A⋅B and B⋅A are different in general, which means that the scalar product of two matrices is noncommutative. In particular, the dimensions of the resulting matrices aren't the same.
The dot product of two vectors — graphical interpretation
Let's take a look at the dot product formula in detail. If we draw both vectors separated by the angle and then try to find the image of the scalar product, we will realize that this consists of the multiplication of two parts: the projection of one vector to the direction of the second one and the same but for the second vector. Since they are both parallel, the result is just the product of their lengths.
As shown in the picture, we can perform the operation in two ways, but the result is always the same. At the conclusion of this section, we can say that the dot product is a multiplication of vectors' lengths projected in the direction of one of them.
The connection of dot product with projections illustrates one of its most important applications in mathematics: studying perpendicularity, also known as orthogonality. Since cos(90°) = 0, the dot product of two vectors is 0 if and only if they are perpendicular to each other. Given two vectors, the easiest way to ascertain their perpendicularity is, therefore, to verify that their product is 0 via componentwise multiplication.
For example, consider the vectors (1, 1), (1, -1). They make the angles of 45° and -45° with the x-axis, and so they are perpendicular to each other. While you can see this by drawing both vectors in the coordinate system, it is much faster to compute their dot product:
(1, 1)⋅(1, -1) = 1 × 1 + 1 × (-1) = 1 - 1 = 0
An opposite case is when we take the dot product of a vector with itself, a² = a⋅a. Since the projection and the vector are the same things, the outcome is the square of the vector's length. In other words, we can find the length of any vector using the square root over the following dot product: |a| = √(a⋅a).
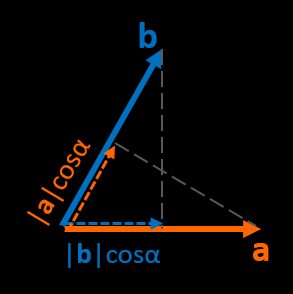
Triple product — how to calculate the volume of a parallelepiped?
Besides the scalar product and the cross product, there is another mathematical tool that makes it possible to provide a calculation for three vectors. We can define a triple product (or mixed product) as a combination of a dot product and a cross product. The formula of the triple product can be expressed as:
V = a⋅(b × c)
b × c is a vector, which means that the overall result is a scalar product of two vectors and is just a number. The letter V isn't a coincidence because there's a direct correlation between the mixed product and the volume. Our volume of a parallelepiped calculator goes deeper into this subject.
Let's look at an example:
- Construct a parallelepiped in the Cartesian coordinate system.
- Denote its sides as
a,b,c— we can interpret them as vectors attached in one point. - The value of
b × c = |b||c| sin αresembles the formula for the area of a parallelogram. As a result, we get the vector whose length is equivalent to the base's area and perpendicular to it. - The last step is to calculate the dot product
a⋅d. As we know from the previous section, it's the projection ofato the direction ofdmultiplied byd. If we take a closer look, we can realize that this projection is actually the height of our polyhedron, and the resulting product is nothing but its volume!
One important remark – the triple product can be estimated in a few equivalent ways:
a⋅(b × c) = b⋅(c × a) = c⋅(a × b)
The crucial thing is that the order a-b-c-a-b-c-... has to be conserved. Otherwise, the result will be negative. We can always circumvent the problem by working out the volume as an absolute value of the triple product.
When both α and β are equal to 90°, the outcome is nothing else but the volume of a rectangular prism!
Applications of dot product
There are several areas where scalar product turns out to be handy.
-
The law of cosines can be proved with the usage of the dot product: If we create a triangle out of 3 vectors, we can write that
c = b - a. If we want to findc², we can expand the formula as follows:c² = (b-a)⋅(b-a)
= b⋅b – b⋅a – a⋅b + a⋅a
= a² + b² - |b| × |a| × cos a - |a| × |b| × cos a
= a² + b² – 2 × |a| × |b| × cos α.The last step is obviously possible because the multiplication of lengths is commutative. And that's it – another way to prove the cosine law!
-
As mentioned at the beginning – the scalar product is the simplest way to find if two vectors are perpendicular to each other.
-
Many physical quantities are defined as scalar products:
- Work as a dot product of force and displacement.
- Power as a scalar product of force and velocity.
- Electric or magnetic flux is a dot product of an electric/magnetic field and the surface it flows through.
- Magnetic potential energy is a scalar product of a magnetic moment and magnetic field.