Volume of a Parallelepiped Calculator

This volume of a parallelepiped calculator will help you calculate the volume of a parallelepiped from its three vectors, four vertices, or edge lengths. Additionally, it will also calculate the area of the parallelepiped. Are you wondering how to find the volume of a parallelepiped formed by three vectors? Do you want to learn the formula for the volume of a parallelepiped with four vertices? Read on to find out the answers to all of these questions and more.

A parallelepiped is a polyhedron whose six faces are parallelograms. To describe a parallelepiped, we need its three adjacent sides and their angles, or the three adjacent vectors.

The formula for the volume of a parallelepiped is given by:

where:

• $V$ — Volume of the parallelepiped formed by the three vectors; and
• $\vec{a}$, $\vec{b}$ and $\vec{c}$ — Three vectors that describe the three adjacent (and unique) sides of a parallelepiped.

The vector multiplication above is called a scalar triple product (or a triple product). It involves the cross product of the vectors $\vec{a}$ and $\vec{b}$, which results in a vector $\vec{a}\times\vec{b}$ perpendicular to both $\vec{a}$ and $\vec{b}$. Check out our cross product calculator if you want to learn more about cross products.

The subsequent dot product between $\vec{a}\times\vec{b}$ and $\vec{c}$ denotes the projection of $\vec{a}\times\vec{b}$ on $\vec{c}$. In other words, it sweeps the parallelogram base along $\vec{c}$, analogous to multiplying the base area with height.

We can further simplify the formula and reduce it to one determinant:

where:

• $a_1$, $a_2$, $a_3$ — Components of $\vec{\bm{a}}$;
• $b_1$, $b_2$, $b_3$ — Components of $\vec{\bm{b}}$;
• $c_1$, $c_2$, $c_3$ — Components of $\vec{\bm{c}}$; and
• $\bm{i}$, $\bm{j}$, $\bm{k}$ — Unit vectors along the coordinate axes.

Our matrix determinant calculator can aid you in understanding and calculating determinants.

Now that you know how to find the volume of a parallelepiped with vectors, let's learn what to do if the only given values are the vertices of the parallelepiped.

You can find any vector between two points from the coordinates of these points using our vector calculator. Once you determine the vectors, you can calculate the parallelepiped volume using the formula above.

To calculate the volume of a parallelepiped formed by the vectors a, b, and c, follow these simple steps:

1. Find the cross-product between the vectors a and b to get a × b.
2. Calculate the dot-product between the vectors a × b and c to get the scalar value (a × b) ∙ c.
3. Determine the volume of the parallelepiped as the absolute value of this scalar, given by ∣(a × b) ∙ c∣.

For example, consider a parallelepiped formed by the vectors $\vec{\bm{a}} = \bm{i} + 2\bm{j} + 3\bm{k}$, $\vec{\bm{b}} = 5\bm{i} - 4\bm{j} + 7\bm{k}$, and $\vec{\bm{c}} = -5\bm{i} + \bm{j} + 12\bm{k}$. Then, the volume of the parallelepiped described by these vectors would be

To calculate the volume of a parallelepiped from its sides (or edge lengths), use the formula V = a∙b∙c∙√(1 + 2∙cos(α)∙cos(β)∙cos(γ) - cos²(α) - cos²(β) - cos²(γ)), where:

• V — Volume of the parallelepiped;
• a, b, and c — Three adjacent sides of the parallelepiped;
• α — Angle between the sides b and c;
• β — Angle between the sides a and c; and
• γ — Angle between the sides a and b.

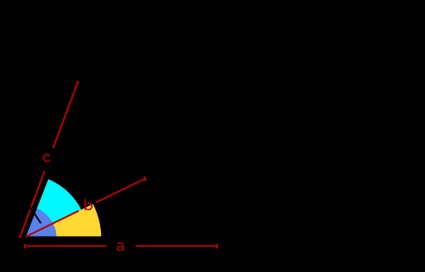
For example, consider a parallelepiped ABCDEFGH with edge lengths $a = 5$, $b = 4$, and $c = 7$. If $\angle \text{DAE} = 45\degree$, $\angle \text{BAD} = 63\degree$ , and $\angle \text{BAE} = 50\degree$, then the volume of the parallelepiped would be V = 5·4·7 √(1 + 2·cos(45)·cos(50)·cos(63) - cos²(45°) - cos²(50°) - cos²(63°) = 75.83.

To calculate the surface area of a parallelepiped formed by the vectors a, b, and c, use the formula A = 2 × (∣a × b∣ + ∣b × c∣ + ∣a × c∣), where:

• ∣a × b∣ — Magnitude of the cross-product between a and b;
• ∣b × c∣ — Magnitude of the cross-product between b and c; and
• ∣a × c∣ — Magnitude of the cross-product between a and c.

Alternatively, you can find the surface area from the edge lengths a, b, and c , using the formula A = 2 × (a∙b∙sin(γ) + b∙c∙sin(α) + a∙c∙sin(β)), where:

• α – Angle between b and c;
• β – Angle between a and c; and
• γ – Angle between a and b.

Note that the magnitude of the cross-product between two vectors $\vec{a}$ and $\vec{b}$, given by $\lvert \vec{a} \times \vec{b} \rvert$ is equal to the area of the parallelogram spanned by these vectors. Hence, adding the magnitudes of the cross-products of the three vectors describing the parallelepiped and multiplying the same by two shall produce its surface area.

For example, consider a parallelepiped ABCDEFGH with edge lengths $a = 5$, $b = 4$, and $c = 7$. If $\angle \text{DAE} = 45\degree$, $\angle \text{BAD} = 63\degree$ , and $\angle \text{BAE} = 50\degree$, then the surface area would be given by

This volume of a parallelepiped calculator is a simple tool and easy to use. It has three different modes of calculation to find the volume of a parallelepiped with 3 vectors, 4 vertices, or using the edge lengths and angles:

1. To calculate the volume of a parallelepiped given 3 vectors:

   • Select the option vectors $a$, $b$ and $c$ in the Calculate using field.
   • Enter the values of the components of each vector.
   • This volume of a parallelepiped calculator will display the calculated volume and surface area of the parallelepiped in the corresponding fields under the Results section.

2. To calculate the volume of a parallelepiped with 4 vertices:

   • Select the option vertices p, q, r, and s in the Calculate using field.
   • Enter the coordinates of each vertex in the corresponding field.
   • The calculator will display the calculated volume and surface area of the parallelepiped in the corresponding fields under the Results section.

3. To calculate the volume of a parallelepiped using the edge lengths:

   • Select the option edge lengths and angles in the Calculate using field.
   • Enter the edge lengths and angles in their corresponding fields.
   • The calculator will display the calculated volume and surface area of the parallelepiped in the corresponding fields under the Results section.