Cross Product Calculator

Without a vector cross product calculator, it is hard to know how to calculate the cross product. Luckily for you, we've made a tool that helps you understand the formula for the cross product of two vectors. We will also be comparing the dot product vs. cross product definitions and explain why they are not the same operation. And as a bonus, we also have a list of practical tricks like the right-hand rule so that you can become a master on how to do the cross product of two vectors.

A vector is a mathematical tool widely used in physics. It allows you to deal with collections of numbers (each representing a dimension) in a very efficient way. The collection of operations, rules, and properties to deal with vectors is called vector algebra and, similarly to the algebra of numbers, it includes multiplication.

However, vectors are more complex than numbers since they carry within them much more information that must be more carefully manipulated. This is one of the reasons why, in vector algebra, there are two different types of multiplications or product operations: the cross product and the dot product. You can compute the latter with the help of our dot product calculator.

The definition, as it is common in mathematics, is very technical. Nevertheless, we will explain what it means in layperson's (and less accurate) terms so that, even if you don't have a strong mathematical background, everything will make sense to you.

One definition of the cross product also called vector product is:

A binary operation on two vectors in three-dimensional space that is denoted by the symbol ×. Given two linearly independent vectors, a and b, the cross product, a × b, is a vector perpendicular to both a and b and thus normal to the plane containing them.

That is indeed a mouthful, but we can translate it from mathematical jargon to a simple explanation. First of all, the definition talks about a three-dimensional space like the one we live in. That's because it is the most common usage of the cross product, but we can extend it to more dimensions; that is, however, beyond the scope of this text and most math-related degrees.

What the definition tells us is that the vector cross product of any two vectors is a third vector that is perpendicular to both of them (and to the plane that contains them). This is possible in 3-dimensional space because, in such space, there are three independent directions. You can think of these three directions as being height, width, and depth.

To know how this new third vector will look in terms of magnitude and mathematical description, we can use the formula for the cross product of two vectors. In the next section, you will be presented with the formal, mathematical formula that tells you how to do the cross product of any two vectors. We will also explain what this equation means and how to use it in a simple yet accurate way.

Before we present the formula for the vector product, we need two vectors that we will call a and b. These two vectors should not be collinear (a.k.a., should not be parallel) for reasons we will explain afterward.

So, without further ado, let's see the formula:

c = a × b = |a| × |b| × sin θ × n

This formula is composed of:

• c – New vector resulting from doing the cross product;
• a – One of the initial vectors;
• b – Second of the initial vectors;
• θ – Angle between both vectors; and
• n – Unit vector perpendicular to a and b simultaneously.

The factor of perpendicularity together with the sinus function present in the formula are good indicators of the geometrical interpretations of the vector cross product. We will talk more about these in the following sections.

You can also see why the two vectors a and b mustn't be parallel. If they were parallel, it would lead to a zero angle between them (θ = 0). Hence, both sin θ and c would be equal to zero, which is a very uninteresting result. Also interesting to note is the fact that a simple permutation of a and b would change only the direction of c since -sin(θ) = sin(-θ).

We have seen the mathematical formula for the vector cross product, but you might still be thinking, "This is all well and good, but how do I actually calculate the new vector?" And that is an excellent question! The fastest and most straightforward solution is to use our vector cross product calculator, but if you have read this far, you are probably looking not only for results but also for knowledge.

We can divide the process into three different steps: calculating the modulus of a vector, calculating the angle between two vectors, and calculating the perpendicular unitary vector. Putting all these three intermediary results together using a simple multiplication will yield the desired vector.

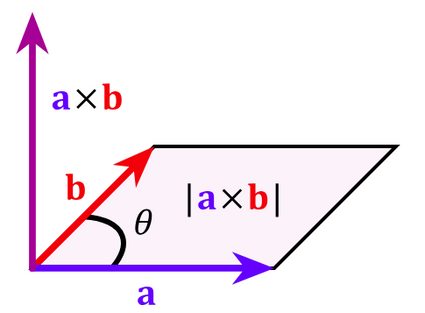
Calculating angles between vectors might get too complicated in 3-D space; and, if all we want to do is to know how to calculate the cross product between two vectors, it might not be worth the hassle. Instead, let's explore a more straightforward and practical way of calculating the vector cross product utilizing a different cross product formula.

This new formula makes use of the decomposition of a 3D vector into its three components. This technic is a very common way to describe and operate with vectors in which each component represents a direction in space and the number accompanying it represents the length of the vector in the specific direction. Canonically, the three dimensions of the 3-D space we're working with are named x, y, and z and are represented by the unitary vectors i, j, and k, respectively.

Following this nomenclature, we can represent each vector by a sum of these three unitary vectors. The vectors are generally omitted for brevities sake but are still implied and have a big bearing on the cross product result. So a vector v can be expressed as: v = (3i + 4j + 1k) or, in short: v = (3, 4, 1) where the position of the numbers matters. Using this notation, we can now understand how to calculate the cross product of two vectors.

We will call our two vectors: v = (v₁, v₂, v₃) and w = (w₁, w₂, w₃). For these two vectors, the formula looks like:

v × w = (v₂w₃ - v₃w₂, v₃w₁ - v₁w₃, v₁w₂ - v₂w₁)

This result might look like a random collection of operations between components of each vector, but nothing is further from reality. For those of you wondering where this all comes from, we encourage you to discover it yourself. All you need to do is start with both vectors expressed as: v = v₁i + v₂j + v₃k and w = w₁i + w₂j + w₃k and multiply each component of a vector with all the components of the other.

As a small hint, we can tell you that when doing the cross product of vectors multiplied by numbers, the result is the "regular" product of the numbers times the cross product between vectors. It will also come in handy to remember that the cross product of parallel vectors (and hence of a vector with itself) is always equal to 0.

After all the things we've talked about, it's time to learn how to use our cross product calculator to save time and obtain results for any two vectors in a 3-D space. As you can see, the variables are divided into three sections, one for each vector involved in a cross product calculation. Of these three vectors, c is probably the one you should care about the most since it is the result of the cross product. Each vector has three components, as mentioned before: x, y, and z, referring to each of the three dimensions: depth, width, and height.

Once we understand what each of the fields does, let's take a quick look at a typical use case for this calculator. To include an example for calculating the cross product of two vectors, we will use the vectors a = (2, 3, 7) and b = (1, 2, 4).

1. The first step is to introduce the components of vector a. That is: x = 2, y = 3 and z = 7.

2. Next, you should introduce the components of vector b. That is: x = 1, y = 2 and z = 4.

3. Now the calculator processes the information; it applies the formula we saw before and...

4. Voilà! You have just calculated:
   c = a × b = (-2, -1, 1).

5. Repeat until you have calculated all the cross products you needed to.

6. Share with your friends the life-changing experience of calculating vector cross products. ;)

You can calculate the cross product of any vectors you want without even having to think about it. However, we highly recommend you to use the properties we have mentioned above for complex operations to save you time and hassle. For example, if one of the vectors is simply a multiple of the other, you don't even need to use our calculator; you can predict that the result will be zero since these two vectors are collinear.

We have explored the most important mathematical aspects of the cross product of two vectors in 3-D space, so it's time to talk about some interesting facts and uses of this vector operation. To kick things off, we will talk about the cousin of the cross product: the dot product.

These two operations have misleadingly similar names but, in fact, represent different concepts in geometry. On top of that, computing the dot product is arguably easier than computing the cross product; nevertheless, we have also made a calculator that helps you calculate the dot product of 2 vectors, also called the scalar product.

Keeping up with the trend of apparent similarities between the scalar product and the cross product, we can take a close look at the formula for the dot product:

v = a ⋅ b = |a| × |b| × cos θ

The only differences between the cross product and the dot product are the trigonometric function used in the formula and the fact that here the result is a number (scalar, hence the name) rather than a vector.

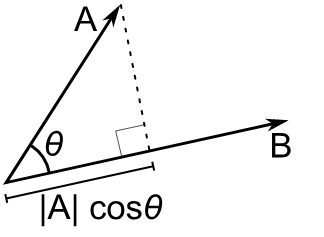
These minor differences might make you believe that both operations are very similar, but they are very different in nature. For starters, the cross product is an operation that takes two vectors and returns another vector perpendicular to both, while the dot product yields a number with no direction. The dot product is more easily generalized to higher or lower dimensions, while the cross product does not even exist in 2-D. Their interpretation in geometric terms is also very different since you can think of the dot product as the length of the projection of one of the vectors onto the other.

All these differences make them very distinct operations conceptually. Therefore, these two operations are not interchangeable or translatable. As we will see in the following sections, both operations are instrumental in both mathematics and physics.

Most of us are not interested in just the purely mathematical properties and uses of the cross product but also in the practical application in the real world. And what better way to get a useful application of mathematical concepts than through physics? The cross product is not an exception; it is a very useful operation in physics. We could get deep into Quantum Field Theory, where both the scalar product and the cross product are widely used.

However, we will stay within the realm of tangible and mathematically perfect theories and look at examples in places and events we can all relate to.

Electromagnetism is the first field we will discuss in which the cross product properties are widely used. In nature, electric and magnetic fields are generally perpendicular to each other, which ties perfectly into how the cross product of two vectors is expressed. Things like calculating the magnetic forces on a current-carrying wire or computations for the magnetic moment of a system all require the use of the cross product operation.

Another example that cannot go unmentioned is the so-called Hall effect, very important in solid-state physics. You can learn about it from the Hall coefficient calculator.

The most common applications of the cross product include investigating the moment of inertia (as in the moment of inertia calculator) and rotating objects. We could have an endless talk about how mind-blowing this part of physics is. Instead, it is better to watch the video where Walter Lewin (one of the best physics educators) explains and demonstrates everything about this phenomenon.

Vectors are ubiquitous in physics; from velocity to weight or even area, everything seems to have a vector associated with it. And that is the reason why the vector cross product is very important in the physical world.

One of the scariest parts of physics is making sense of all the mathematical work one has to do to calculate almost anything. As we include vectors and several dimensions, this can quickly become an uncontrollable mess that seems not to have anything to do with reality. To solve these problems, physicists have developed some tricks to help you navigate these muddy waters.

Probably the most known one is the "Right-hand rule", which helps in the cross vector product calculation. This rule enables you to predict where the resulting vector of the cross product will be directed by only using your hand.

There are two versions of the right-hand rule in physics: one with the fingers extended and the hand still, and the other involving going from an open hand to a closed fist.

The first version (more common) consists of spreading the middle and index finger, as shown in the picture above. With the thumb extended, you should aim at aligning the index finger with the first vector and the middle finger with the second one. In this position, the extended thumb will show the direction of the resulting vector from computing the vector cross product.

The second method is, in our opinion, easier to use. With an open hand, you align the fingers with the first vector. Then, you close your hand into a fist towards the second vector. After performing these actions, you will end up with a thumbs-up or thumbs-down hand. As in the previous case, the direction of the thumb will indicate the direction of the vector resulting from the cross product operation.

All these might seem like childish games, but they are potent tricks. With a simple hand gesture, you can get a nonadulterated perspective on how the vector cross product will look like. It might even come as a surprise to you that these tricks are continuously used by researchers whenever their work involves any cross product calculations, like when utilizing the formula from the Lorentz force calculator.