Vector Calculator
Welcome to our vector calculator! It'll help you perform and understand a whole bunch of vector operations. Do you have the Cartesian coordinates of two vectors, or just know their vector direction and magnitude? Maybe you need to find the vector between two points? This vector calculator can deal with all those situations; it performs:
- Vector addition;
- Vector subtraction;
- Vector multiplication (both cross product and dot product!); and
- Vector projections.
As a bonus, we'll also teach you what the norm of a vector is and how to normalize a vector.
Cartesian coordinates
In a rectangular (called Cartesian) xy-coordinate system, we describe vector a in a 2D plane by its Cartesian coordinates:
a = [ax, ay].
These coordinates correspond to the fact that we can decompose a displacement along vector a into horizontal displacement ax along x-axis and vertical displacement ay along the y-axis.
Similarly, we describe vectors in 3D-space using the Cartesian xyz-system with three numbers:
a = [ax, ay, az],
which correspond to displacements along the x-, y-, and z-axis, respectively.
Vector direction and magnitude
We can also describe a plane vector in terms of vector direction and magnitude. The magnitude of a vector is its length (also called the norm) and the direction of a vector is the angle between the horizontal axis and the vector.
Let [ax, ay] be the Cartesian coordinates of a vector with magnitude m and direction θ. To convert one set of coordinates to the other, use the following formulas:
ax = m × cos(θ)
ay = m × sin(θ)
How to determine a vector between two points?
If you need to determine a vector between two points, i.e., from the initial and final point, just subtract the coordinates of the final point from the initial point:
-
Initial point (origin): a = [ax, ay, az]
-
Final point (tip/head): b = [bx, by, bz]
-
Vector between these two points:
[bx - ax, by - ay, bz - az]
Let's have a look at an example:
-
Initial point:
[1, 2, 3] -
Final point:
[1, 1, -1] -
Vector between these two points:
[1 - 1, 1 - 2, 3 - (-1)] = [0, -1, 4]
How to normalize a vector? What is the norm of a vector?
Vector normalization is just squeezing/stretching a vector so that it has unit magnitude. Remember that a vector's direction must be kept!
To normalize a vector, find its norm using the Pythagorean theorem. The norm of a vector is its magnitude: the square root of the sum of the squared coordinates of your vector. Then divide each coordinate of the initial vector by this norm. You may also want to use the vector magnitude calculator to find the norm, which is the simpler version of this vector calculator.
Example:
Let a = [2, 3, 4]. Let us find the norm of a:
|a| = √(4 + 9 + 16) = √29
Normalization of a gives us the vector a/|a| = [2/√29, 3√29, 4/√29]. Do you know that we have a dedicated calculator for normalizing vectors?
How to use this vector calculator?
To use the vector calculator, simply follow the steps below:
- Tell us whether you are working with plane (2D) or space (3D) vectors.
- Decide on the vector operation you want to perform. You can choose vector addition or subtraction, vector multiplication (dot or cross product), normalization, vector projection, or finding the vector between two points.
- Enter your data. You may choose between Cartesian coordinates or vector direction & magnitude in the case of plane vectors.
- Our vector calculator returns the results immediately. Enjoy! 😊
Vector addition
-
In Cartesian coordinates, we can perform vector addition simply by adding the corresponding components of the vectors:
for a = [ax, ay, az],
and b = [bx, by, bz],
we have a + b = [ax + bx, ay + by, az + bz].
Example:
The sum of
a = [2, 3, 4]andb = [1, -2, 3]is:a + b = [2 + 1, 3 + (-2), 4 + 3] = [3, 1, 7] -
Graphical method: for two vectors
aandb, if we want to obtain the vector suma + b, place the origin ofbto the tip ofa. The resulting vector goes from the origin ofato the tip ofb. We call this rule the parallelogram law:
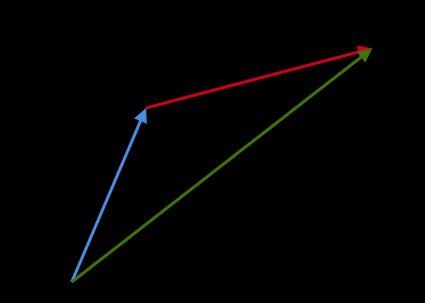
Vector subtraction
The subtraction of vector b from vector a is just the addition of -b to a. To find vector -b, take the coordinates of b with opposite signs; change pluses to minuses and minuses to pluses:
if b = [1, -2, 4],
then -b = [-1, 2, -4]
-
Consequently, in Cartesian coordinates, we perform vector subtraction
a - bby subtracting the coordinates ofbfrom those ofa:if a = [ax, ay, az]
and b = [bx, by, bz],
then a - b = [ax - bx, ay - by, az - bz].
Example:
The difference of
a = [2, 3, 4]andb = [1, -2, 3]is given bya - b = [2 - 1, 3 - (-2), 4 - 3] = [1, 5, 1]. -
Graphical method: we obtain the vector difference
a - bby placing the tip ofbto the tip ofaand drawing a vector from the origin ofato the origin ofb:
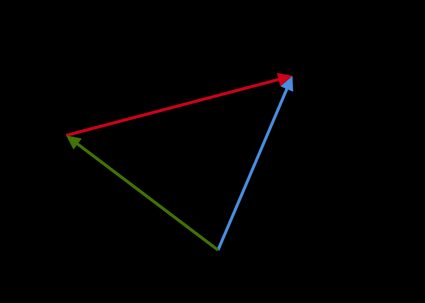
Vector multiplication
Be careful when asked to multiply vectors — there are several different types of vector multiplication! The most popular are the cross product and dot product, which we describe below:
Vector multiplication - Cross product
The cross product is an operation denoted by the operator × and takes two vectors and returns another vector.
The formula is as follows:
a × b = |a| × |b| × sin(θ) × n,
where:
θ— Angle betweenaandb;|a|and|b|— Magnitudes ofaandb; andn— Unit vector perpendicular to bothaandb, determined by the Right Hand Rule.
Right Hand Rule:
Position your right hand so that your index finger points along vector
aand your middle finger points along vectorb: your thumb shows the direction of the cross producta × b.
- Graphical interpretation: The resulting vector
a × bis at a right angle (perpendicular) to the initial vectors, and its magnitude is equal to the area of a parallelogram spanned by the initial vectors:
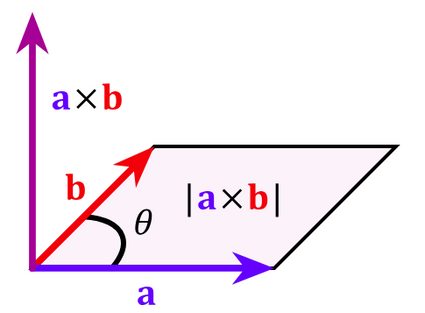
-
In terms of Cartesian coordinates:
for a = [ax, ay, az],
and b = [bx, by, bz], we have
a × b = [ay×bz - az×by, az×bx - ax×bz, ax×by - ay×bx].
Example:
The cross product of
a = [2, 3, 4]andb = [1, -2, 3]is equal toa × b = [3 × 3 - 4 × (-2), 4 × 1 - 2 × 3, 2 × (-2) - 3 × 1] = [17, -2, -7]. -
Yes, the formula looks a bit intimidating. It is easier to remember it once you realize that the coordinates of the product are the determinants of the appropriate 2 x 2 matrices:
- The first coordinate is:

- The second coordinate is:

- The third coordinate is:

-
Be careful with the order of vectors because, in contrast to the dot product, the order matters for the cross product! More precisely, we have
b × a = - a × b, so if you had the order wrong, just change the sign, and you'll be all right 🙃 -
You can find more details and interesting information about the cross product in our article titled "Cross Product of Two Vectors".
-
The vector cross product has lots of applications in physics & engineering – e.g., you can use it to determine the Lorentz force. Go check our cross product calculator to find out more!
Vector multiplication - Dot product
The dot product (also known as the scalar product) is an operation denoted by the operator · that takes two vectors and returns a number. For two vectors a and b, their dot product is the product of their magnitudes (norms) |a| and |b| and the cosine of the angle θ between them:
a · b = |a| × |b| × cos(θ).
-
In Cartesian coordinates, the dot product is the sum of the products of the corresponding coordinates of your two vectors:
a · b = ax × bx + ay × by + az × bz
Example:
The dot product of
a = [2, 3, 4]andb = [1, -2, 3]isa · b = 2 × 1 + 3 × (-2) + 4 × 3 = 2 - 6 + 12 = 8. -
As you may have already concluded from the formula, order does not matter here:
a · b = b · a. -
Tip: if you calculate the dot product of a vector with itself, you arrive at a squared magnitude of the vector:
a · a = |a|²! -
For more details, check our dedicated dot product calculator.
Vector projection
The projection of b onto a is the vector which is the best approximation of b among the vectors obtained by stretching and squeezing vector a. Hence, to find the projection, you just need to know the proper stretching/squeezing factor.
-
Formula:
The projection of
bonais vectorascaled by:a · b / |a|².Example:
Let
a = [2, 3, 4]andb = [1, -2, 3]. Let's calculate the projection ofbontoa. First, let's find the scaling factor. We have calculated above thata · b = 8and|a| = √29. Consequently, the projection ofbontoais:8/29 * [2, 3, 4] = [16/29, 24/29, 32/29] -
To find the projection of
bontoagraphically, you need to decomposebalong the axes spanned byaand perpendicular toa. The component that lies alongsideais the projection ofbontoa. You may also think of this as the shadow that vectorbwould cast on vectoraif there were a light source hung above these vectors:
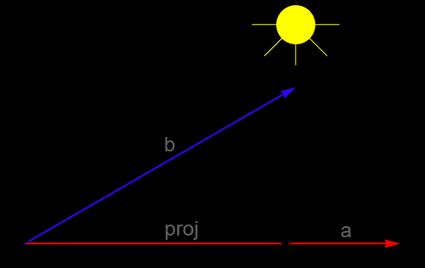
To learn more about projecting vectors onto other vectors, go to our dedicated vector projection calculator.
FAQs
What is a vector?
A vector is a mathematical object defined by:
- A magnitude; and
- A direction.
They are substantially different than scalar quantities: the latter doesn't change with the direction.
Vectors have widespread applications in physics, where they fit quantities such as displacement and velocity.
How do I find the projection of a vector onto another?
If you consider the vectors a and b, you can find the projection of a onto b by following the next steps:
- Calculate the dot product between
aandb:a · b. - Calculate the dot product of
bby itself:b · b. - Calculate the ratio between the two results:
(a · b)/(b · b). - Multiply the result (a scalar) by the vector
b:[(a · b)/(b · b)] × b.
What is the scalar product of two vectors?
The scalar product of two vectors is an operation that consists of summing the product of the components of two vectors "dimension-wise".
If you have two vectors, a = (a₁, a₂, a₃, ..., an) and b = (b₁, b₂, b₃, ..., bn), follow these two steps to compute the scalar product:
- Calculate the product of each pair of components: a₁ × b₁, a₂ × b₂, etc.
- Sum the results: (a₁ × b₁) + (a₂ × b₂).
Notice that you can only compute the scalar product of vectors with the same number of components.
What is the magnitude of a vector with components (3,1,4,1,5)?
To compute the magnitude of the vector with components (3,1,4,1,5), apply the generalized Pythagorean theorem over all the components. If the vector is a = (a₁, a₂, a₃, ..., an), we found the magnitude with the formula:
||a|| = √(a₁² + a₂² + a₃² + ... + an²)
In the case of the vector (3,1,4,1,5), the magnitude is:
√(3² + 1² + 4² + 1² + 5²) = √(9+1+16+1+25) = √(52) ≈ 7.21
