Vector Addition Calculator

Welcome to Omni's vector addition calculator, where we'll learn all about adding vectors in 2D or 3D. Our tool allows us to give the two vectors using Cartesian coordinates or the magnitude and angle. As a bonus feature, it can take some multiples of the vectors or function as a vector subtraction calculator. And for times when you don't have Omni's tool at hand, we give the vector addition formula and describe in detail how to add vectors using the parallelogram rule.

Prefer watching rather than reading? Check out our video lesson on vector subtraction and addition here:

From a mathematical point of view, a vector is an ordered sequence of numbers (a pair in 2D, a triple in 3D, and more in higher dimensions), and that's all there is to it. Of course, scientists wouldn't be themselves if they left it at that, so they expanded this definition. In general, a vector is an element of a vector space, period. This explanation seems simple enough until we learn that, for mathematicians, vector spaces can consist of sequences, functions, permutations, matrices, etc. Fortunately, we need none of that in this vector addition calculator.

On the other hand, physicists prefer to think of vectors as arrows (which are their visual representation) attached to objects. As such, they represent forces that act upon an object, be it gravitation, brake force, or magnetic pull. The direction of such an arrow tells us the force's... well, direction, while its length indicates how large of a force it is.

Fortunately, both approaches are essentially the same thing, at least in our case and in this vector addition calculator. Still, we can represent vectors in two ways: using Cartesian coordinates or the magnitude and angle. However, the latter is possible only in the two-dimensional case since it corresponds, in fact, to having polar coordinates.

Let's look at an example. A vector v= (2,1) lives in 2D (since it has two coordinates) and tells us, in essence, that "it goes two steps along the X-axis and one step along the Y-axis." Note that positive coordinates translate to traveling to the right and upwards (along the horizontal and vertical axis, respectively), while negative indicates the opposite direction. Similarly, if we add a third coordinate, say, w= (2,1,5), we'll end up in 3D, and the extra 5 corresponds to movement along the Z-axis.

Alternatively, we can represent the two-dimensional vector v using its magnitude m and direction θ. The first one is simply the vector's length. The latter is the angle going counterclockwise from the positive half of the horizontal axis to the vector when drawn on the plane with the start point in (0,0).

In particular, this means that m must be non-negative, while θ should be between 0 and 360 degrees (or between 0 and 2π in radians), although this adding vectors calculator accepts other values of the angle according to the same rules which govern trigonometric functions and their arguments.

Let us mention that there does exist an equivalent of polar coordinates (magnitude and direction) in 3D called spherical coordinates. Nevertheless, they tend to be messy and are far less common in practice, so we skip them in our vector addition calculator. Still, you can learn more about them in our spherical coordinates calculator.

Alright, we've come to know the object we're dealing with quite well. It's time to take a couple of them and see a description of how to add vectors.

Adding vectors is easy, especially when we have Cartesian coordinates. To be precise, we simply add the numbers coordinate-wise. That means that the vector addition formula in 2D is as follows:

(a,b) + (d,e) = (a + d, b + e),

and the one in 3D is

(a,b,c) + (d,e,f) = (a + d, b + e, c + f).

That's all there is to it, no strings attached. It's nice to have a simple formula for a change, isn't it?

In 2D, if we use the magnitude and direction representation, the thing gets slightly more complicated. Unfortunately, in this case, we can't just add the values of the two vectors as we did with Cartesian coordinates. We give an excellent visual explanation of why it is so by using the parallelogram law in the next section.

However, suppose you don't feel like drawing the vectors. In that case, the best way to find their sum in this form is to simply find their representation in Cartesian coordinates and use the vector addition formula from the beginning of this section.

Certainly, it helps that the transition from one to the other is relatively simple. To be precise, if a vector v has magnitude m and direction θ, then v= (x,y) in Cartesian coordinates with:

x = m × cos(θ) and y = m × sin(θ),

where cos and sin are the cosine and sine trigonometric functions, respectively (learn more about them in the trigonometric functions calculator). For completeness, let us also mention the transition formula from polar coordinates to Cartesian ones:

m = √(x² + y²) and θ = arccos(x / m),

where arccos is the inverse cosine function (more about it in our arccos calculator).

Before we show you the parallelogram rule, let's mention a couple of bonus functionalities of the vector addition calculator.

1. Vector subtraction calculator
   We give it such a fancy name, but it boils down to a super simple change. To be precise, instead of adding vectors, you might want to find their difference. The rules are the same as before: we subtract the vectors coordinate-wise. To use this option, simply choose Subtraction under Operation in the tool, and the thing will change into a vector subtraction calculator.

2. Adding vectors with multiples
   It may happen that you'd like to add a vector not once but several times. For instance, v+ 4 ×w would mean adding four copies of w to v. Instead of using the vector addition calculator four times to find the result, you can change without multiples to with multiples and input the values of α and β. Of course, you can combine this option with point 1. and have yourself a vector subtraction calculator with multiples.

In the first section, we've mentioned that we represent vectors as arrows. So far, we've only dealt with them algebraically, like in the vector addition formula. It's now time to get back to drawings. Drawing parallelograms, to be precise.

In essence, adding vectors means traveling along one of them and then the other. That means that if we draw one as an arrow, then the "traveling" along it translates to moving (as a point) from its starting point to the endpoint. If we want to move with the second one from there, we can simply draw it beginning at the first endpoint, and the place where that arrow points would be our result.

Above, we've described the idea behind adding vectors visually, and it is also what the parallelogram rule relies on. It's just a more fancy way of putting it. Namely: the sum of two vectors is the diagonal of a parallelogram whose sides are the two added vectors when drawn coming out of the same point.

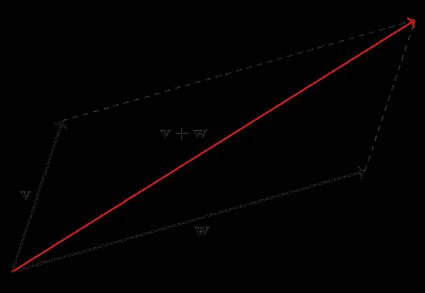
In the picture, we can move from the vertex where v and w start to the opposite vertex by traveling first along v and then w, or vice versa (the second step is then drawn by a dashed line). That is the same as we've done at the beginning of this section. Also, note how the order in which we travel doesn't really matter because addition is commutative.

And with that, we conclude the theoretical part for today. Now we move on to use all that knowledge and see how the vector addition calculator works in practice.

Suppose that we'd like to find the sum of a vector v= (-3,2,8) and three copies of w= (2,2,-4). Before we do it by hand, let's see how we can use the vector addition calculator to find the answer.

Firstly, note that we're adding vectors with three (Cartesian) coordinates, so they're three-dimensional. Therefore, we need to choose "3D" under "Vectors in" and "Addition" under "Operation." That will show us two sections for the coordinates, each with three variable fields marked x, y, and z, which correspond to the first, second, and third coordinates, respectively. Therefore, in the section describing v = (-3,2,8), we input:

x = -3, y = 2, z = 8,

and in that of w= (2,2,-4), we write:

x = 2, y = 2, z = -4.

Once we input the last value, we can see v + w in the "Result" section. However, that's not really what we need, is it? We'd like to add three copies of w and not one.

Therefore, we choose the option "with multiples" at the top of the calculator, which will calculate α ×v+ β ×w instead of only v + w. Note how we already have α = 1 and β = 1 input there as default. For our problem, we change it to:

α = 1, β = 3,

which will give us the final solution. However, before we reveal it, let's use the vector addition formula and find the sum ourselves.

Observe that adding three copies of a vector translates to adding three times its coordinates. Therefore,

v+ 3 ×w= (-3,2,8) + 3 × (2,2,-4) = (-3 + 3 × 2, 2 + 3 × 2, 8 + 3 × (-4)) = (3,8,-4).

Voilà! That might have been a single line of calculations, but can you imagine doing all this with some terribly complicated entries? Well, it's a good thing we have Omni's vector addition calculator to save us time and trouble.