Last updated: Jul 25, 2024

Polar Coordinates Calculator

Q: How do I convert from Cartesian to polar?

If you know the Cartesian coordinates (x,y) of a point and want to express them as polar coordinates (r,θ) , use the following formulas: r = √(x² + y²) and θ = arctan(y/x) Remember the polar coordinates are subject to the following constraints: r must be greater than or equal to 0; and θ has to lie within the range (−π, π].

Q: How do I convert from polar to Cartesian?

To go from the polar coordinates (r,θ) of a point to the Cartesian coordinates (x,y) , simply use the following equations: x = r × cos θ and y = r × sin θ

Q: Can all Cartesian coordinates be written as polar coordinates?

Yes , every point (x,y) in the Cartesian plane can be converted to polar coordinates (r,θ) .

Q: What is the polar form of the Cartesian point (0,0)?

The polar form of (0,0) is not unique, because every polar point (0,ϕ) represents the Cartesian point (0,0) . However, by convention, we often choose (0,0) as the polar coordinates of the Cartesian point (0,0) .

New

Table of contents

Cartesian and polar coordinates How do I convert from Cartesian to polar?How do I convert from polar to Cartesian?FAQs

This polar coordinates calculator is a handy tool that allows you to convert Cartesian to polar coordinates, as well as the other way around. It is applicable only in a 2D space – for 3D coordinates, you might want to head to our cylindrical coordinates calculator. This article will provide you with a short explanation of both types of coordinates and formulas for quick conversion.

Cartesian and polar coordinates

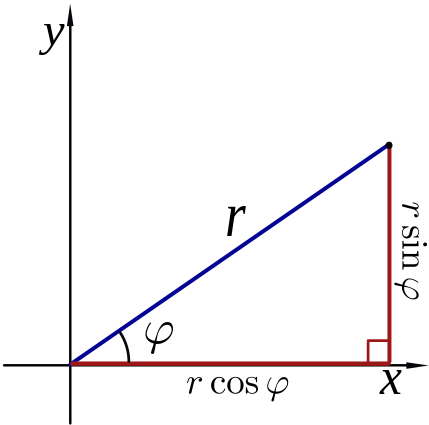
As you probably know, we use coordinates to describe the position of a point in space uniquely. For now, we will limit ourselves to a 2D space. It means that we only have two dimensions: height and width (no depth), just as on a piece of paper.

The Cartesian coordinate system is created by drawing two perpendicular lines. Then, the point where they meet is called the origin of the coordinate system. Coordinates of any arbitrary point in space are the distances between this point and the two lines, denoted by the x-axis and the y-axis. You can learn more about calculating the distance between two points with our distance calculator.

On the other hand, the polar coordinate system does not include any perpendicular lines. The origin of the polar system is a point called the pole. An arbitrary ray from this point is chosen to be the polar axis. To find the polar coordinates of a given point, you first have to draw a line joining it with the pole. Then, the point's coordinates are the length of this line r and the angle θ it makes with the polar axis.

Our polar coordinates calculator can convert both ways between Cartesian and polar coordinates. It assumes that the origin of the Cartesian system overlaps with the pole of the polar system.

How do I convert from Cartesian to polar?

If you know the Cartesian coordinates (x,y) of a point and want to express them as polar coordinates (r,θ), use the following formulas:

r = √(x² + y²) and θ = arctan(y/x)

Remember the polar coordinates are subject to the following constraints:

r must be greater than or equal to 0; and
θ has to lie within the range (−π, π].

How do I convert from polar to Cartesian?

To go from the polar coordinates (r,θ) of a point to the Cartesian coordinates (x,y), simply use the following equations:

x = r × cos θ and y = r × sin θ

You can notice that the value y/x is the slope of the line joining the pole and the arbitrary point.

🙋 You might also be interested in our spherical coordinates calculator and slope calculator.

FAQs

Can all Cartesian coordinates be written as polar coordinates?

Yes, every point (x,y) in the Cartesian plane can be converted to polar coordinates (r,θ).

What is the polar form of the Cartesian point (0,0)?

The polar form of (0,0) is not unique, because every polar point (0,ϕ) represents the Cartesian point (0,0). However, by convention, we often choose (0,0) as the polar coordinates of the Cartesian point (0,0).

What is the polar point (2,π) in Cartesian coordinates?

To convert from polar to Cartesian coordinates:

Recall the conversion formulas x = r × cos θ and y = r × sin θ.
Compute sin(π) = 0 and cos(π) = -1.
So we get x = 2 × (-1) and y = 2 × 0
We arrive at the Cartesian coordinates (-2,0).