Angle Conversion Calculator
With this angle converter, you can quickly check the size of an angle in ten different units:
- degrees, minutes of arc and seconds of arc;
- degrees (deg);
- radians (rad);
- gradians (gon);
- turns (tr);
- π radians (*π rad);
- minutes of arc (arcmin);
- seconds of arc (arcsec);
- milliradians (mrad); and
- microradians (μrad).
Would you like to learn how to convert degrees to radians, and learn the radians to degrees formula? Then keep reading! We will also explain what an acute and obtuse angle is, and answer the question of the hour: what is an angle?
What is an angle? - acute, obtuse angles
An angle is a figure formed by two rays that share a starting point, called a vertex. You may ask: why are angles useful? You can estimate the height of a tower if you know its distance from you, and the angle between the ground and the tower's top. Using the same technique, you can measure how big the moon is, or, with the right equipment, the circumference of our own planet. Also, if you throw something, and you want to know how far it will travel, you'll need to know the angle you throw it at. There are many other fields where angles are useful, but, for now, let's focus on basic geometry. We can divide angles by their size:
| Angle type | Degrees | Radians | Turns | Gradians | Picture |
|---|---|---|---|---|---|
| Acute | between 0° - 90° | between 0 - ½π | between 0 - ¼ | between 0g - 100g |  |
| Right | 90° | ½π | ¼ | 100g |  |
| Obtuse | between 90° - 180° | between ½π - π | between ¼ - ½ | between 100g - 200g |  |
| Straight | 180° | π | ½ | 200g |  |
| Reflex | between 180° - 360° | between π - 2π | between ½ - 1 | between 200g - 400g |  |
| Full (Perigon) | 360° | 2π | 1 | 400g |  |
But there are other ways to group angles. Some of them are:
- Complementary angles - two angles that add up to a right angle (90°);
- Supplementary angles - combined angle pair equals 180° (straight angle);
- Reference angle - a acute angle that represents any other angle. Don't hesitate to learn more in the reference angle calculator; and
- Central angle - an angle with a vertex at the center of a circle, whose arms extend to the cirlce's circumference.
What is a radian and how to convert degrees to radians?
The radian is the most universal unit for measuring angles. 1 radian is equal to about 57.2958 degrees, which is the angle that creates an arc equal to the length of the radius, R:
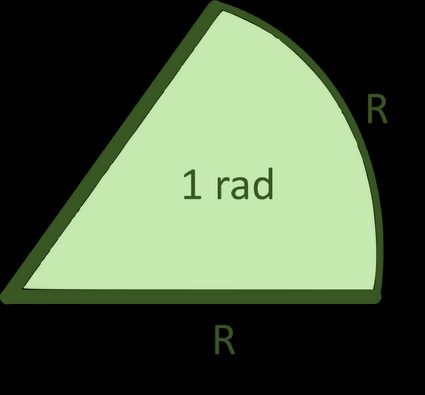
A full turn is equal to 2π radians, which is why the circumference is equal to 2πR. To make things easier for you, we created a table with the most common angles:
| Degrees | Radians |
|---|---|
| 15° | π/12 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
As you see, 180 degrees is equal to π radians, so the degrees to radians formula is:
radians = π/180° * degrees
That means the radians to degrees formula is predictable:
degrees = 180°/π * radians
Let's look at an example: What is a 300° angle in radians?
radians = π/180° * 300° = ⁵⁄₃π rad
And now you know how to convert degrees to radians!
How to convert degrees minutes seconds to decimal degrees?
Minutes of arc and seconds of arc are sometimes used alongside degrees. For example, they're often used to specify coordinates. How to convert DMS (degrees minutes seconds) to decimal degrees, then? The answer is straightforward, think about degrees like hours. One hour equals sixty minutes, and one degree equals sixty minutes. In both cases, each minute contains sixty seconds. So one degree equals 3600 seconds:
1 degree = 60 minutes of arc = 3600 seconds of arc
When you realize that, figuring out the formula is easy:
Decimal degrees = degrees + minutes/60 + seconds/3600
Let's say you want to figure out what 48°37'45" is in decimal degrees:
48°37'52" = 48 + 37/60 + 52/3600 = 48.6311°
So 48°37'45" is the same as 48.6311°.
Other units
To describe the size of an angle, you usually use degrees or radians. However, there are other units that you might come across. One of them is a turn. One turn equals 360 degrees, or 2π radians. To convert between these units, use one of the formulas below:
- Degrees to turns formula:
turn = degrees / 360°; and - Radians to turns equation:
turn = radians / 2π.
A less common unit is called a gradian, or a gon. In this case, one gradian is defined as one-hundredth of the right angle. The degrees to gradians formula is:
gradians = ⁹⁄₁₀ * degrees
To convert radians to gradians, use this equation:
gradians = π/200 * radians
And to switch turns into gradians:
gradians = ¹⁄₄₀₀ * turns
Now you know how to convert between different angular units. To learn more about geometry, check out the triangle area calculator, or any of our other geometry calculators!
