Height of a Square Pyramid Calculator
Table of contents
Height of a square pyramidHow to find the height of a square pyramidHow to use the height of a square pyramid calculatorOther related calculatorsFAQsWelcome to the height of a square pyramid calculator! This calculator, which focuses on determining the height (H) of a right square pyramid, is part of our calculator series that deals with different types of pyramids. In this calculator, you will learn:
- How to find the height of a square pyramid;
- The pyramid dimensions you need to calculate H; and
- The different formulas to find H.
Keep on reading to start learning 🙂.
⚠️ Take note, however, that this height of a square pyramid calculator only calculates the height of regular or right square pyramids where the pyramid's vertex lies directly above the center of the pyramid's square base.
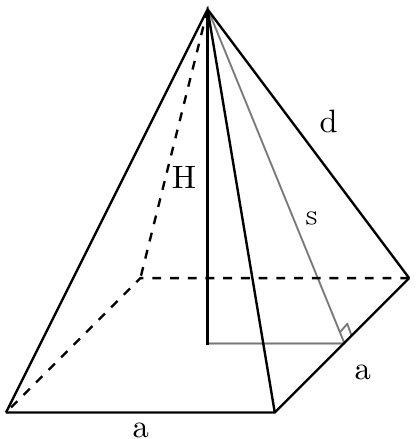
Height of a square pyramid
The height of a square pyramid, also called altitude, is the perpendicular distance between its base and its vertex. When asked how tall a pyramid is, the pyramid's height is what we find.
Since pyramids are solid figures, they have volume. And we can use that to determine the height of a pyramid.
How to find the height of a square pyramid
It is easy to determine the height of a square pyramid when you know its volume and base area. You simply have to multiply the volume by three and divide everything by the base area, as shown in the formula below:
H = 3 × V / A_b
where:
His the height of the pyramid;Vis the volume of the pyramid; andA_bis the pyramid's base area.
Since the base area is equal to the square of the base edge, A_b = a², we can also express the equation above in terms of V and a like this:
H = 3 × V / a²
As you may have noticed, to find the height of the right pyramid, we would need the base edge, a, and a parameter that indicates that the pyramid is a solid figure. Those parameters include the pyramid's volume (as described above), slant height (s), and lateral edge (d). You can learn more about these dimensions in our right square pyramid calculator.
If you know a right square pyramid's base edge length and slant height, you can use this formula to find H:
H = √(s² - (a / 2)²)
On the other hand, if you can measure its lateral edge, this is what you can use:
H = √(d² - a² / 2)
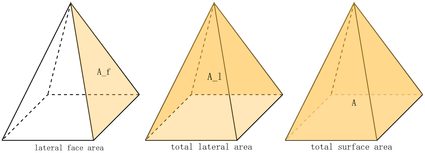
The formulas above are pretty much what you need to find H in most situations. However, sometimes we're not given the values for such parameters. So here are the formulas for the lateral face area (A_f), total lateral area (A_l), and total surface area (A) that you can use to extract the value of the slant height, given the base edge, a:
-
A_f = a × s / 2 -
A_l = 2 × a × s -
A = a² + 2 × a × s
🙋 Please note that you should have at least the value for the base edge, a, or have a way to calculate its value to find H. Let's say you're given the values for d and s; you can utilize the Pythagorean theorem to have a = 2 × √(d² - s²) and use that to determine the height of your right square pyramid.
How to use the height of a square pyramid calculator
This height of the square pyramid calculator is very straightforward to use.
- The first step is to select which pair of measurements you want to use to find H.
- Then, enter those measurements' values. Instantly, you'll get your pyramid's height.
- If you want to see every measurement and play around with the calculator, select
any custom pairsin the options.
🙋 Before entering a new set of data, please click on the reload button ⟳ below our calculator to avoid errors.
What is the height of the square pyramid entrance at the Louvre Museum?
The Louvre Pyramid is about 21.6 meters (70.9 ft) high. We can also find its height using these steps:
- First, measure its base edge length to get around 35.0 m (114.8 ft).
- Try to measure its slant height where we'll obtain 27.8 m (91.2 ft).
- Use the Pythagorean Theorem, H = √(s² - (a / 2)²) = √(27.8² - (35 / 2)²) = 21.6 m
How to calculate the height of a square pyramid?
Given the volume and base edge of a pyramid, you can follow these steps to calculate the pyramid height:
- First, square the base edge to find the base area.
- Then, divide the known volume by the base area.
- Finally, multiply the obtained quotient by 3 to get the pyramid height.
