Omni Calculator logo
Last updated:

Pyramid Angle Calculator

New

Table of contents

What is a pyramid?The angles of a pyramidHow to calculate the pyramid anglesHow to calculate the angles of a square pyramidHow to use our pyramid angle calculatorFAQs

Use our pyramid angle calculator to find all the possible angles in a pyramid - we'll ask you a few parameters, and do all the math for you!

Here you will learn:

  • The types of angles in a pyramid;
  • How to calculate the angles of a pyramid;
  • An example of how to calculate the square pyramid angles; and
  • How to use our pyramid angle calculator.

What is a pyramid?

A pyramid is a solid figure with a polygonal base. A triangular face corresponds to each side of the base, joining at the apex.

The base can be of any shape; however, regular pyramids are easier to study. The base of a regular pyramid is a regular polygon. We can find, for example:

  • Triangular pyramids, with an equilateral triangle as the base;
  • Square pyramids, where the base is, of course, a square;
  • Hexagonal pyramids; and
  • Well, infinitely more.

If the apex lies above the centroid of the base (the geometric mean point of the polygon), we call the pyramid a right pyramid; otherwise, we have an oblique pyramid. Here we will analyze only right pyramids.

💡 We have many pyramid calculators here at Omni: check out our pyramid volume calculator, our right rectangular pyramid calculator, and our triangular pyramid volume calculator!

The angles of a pyramid

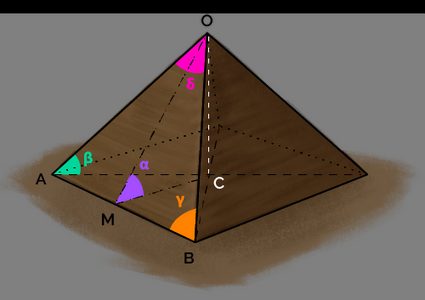
There are a lot of angles in a pyramid, but luckily in a regular pyramid, most of them are identical. Let's identify them!

We can identify the angle between the faces' vertical medians and the base at the apex. It defines how "slender" a pyramid is. We call this angle α\alpha.

The angle between the edge and the base β\beta is always smaller than α\alpha in pyramids with a convex base: the corner of the base is farther from the centroid than the center of its sides.

Pyramid diagram
The angles of a hexagonal pyramid. You can identify analogue angles in other regular pyramids

We can identify other angles, also related to the pyramid's height. They lie on each face, and since in a regular pyramid a face is an isosceles triangle, the two angles at the bottom are identical. We identify them with the letter γ\gamma. The angle on the top, at the apex, gets smaller for tall and slender pyramids. We call it δ\delta.

We highlighted α\alpha and β\beta in a hexagonal pyramid (because hexagons are the bestagons).

Now you know which angles to search for. It's time to learn how to calculate the angles in a pyramid!

How to calculate the pyramid angles

To find the angles we need to use a bit of trigonometry - in particular the theorems to find the elements of a right triangle.

Let's start with the angle α\alpha, between the median of a face and the base. Let's take a look at the diagram, now marked with some relevant points.

α\alpha corresponds to the angle CM^O\text{C}\widehat{\text{M}}\text{O}. We compute it noting that the catheti of the triangles are OC\text{OC} (the height of the pyramid) and CM\text{CM} (the segment from the side's midpoint to the centroid). We calculate the angle α\alpha with:

tan⁡α=OCCM → α=arctan⁡(OCCM)\footnotesize \tan{\alpha} = \frac{\text{OC}}{\text{CM}} \ \rightarrow \ \alpha = \arctan{\left(\frac{\text{OC}}{\text{CM}}\right)}

Let's proceed with the angle β\beta. In this case, we need to use the segment AC\text{AC} to compute the tangent:

tan⁡β=OCAC → β=arctan⁡(OCAC)\footnotesize \tan{\beta} = \frac{\text{OC}}{\text{AC}}\ \rightarrow\ \beta= \arctan{\left(\frac{\text{OC}}{\text{AC}}\right)}

🔎 Note that AC>CM\text{AC}>\text{CM} is always true: this explains why β<α\beta<\alpha.

It's time to compute the angle on a pyramid's face. Using the old and reliable Pythagorean theorem, we find the length of the slanted side of the pyramid:

🙋 To analyze these angles, we move to the other side of the base! Take another look at the diagram if you have trouble visualizing the equations.

PO=OC2+PC2\text{PO}=\sqrt{\text{OC}^2+\text{PC}^2}

On each face, we can identify a pair of right triangles created by the median (in this case ON\text{ON}). The segment PN\text{PN} (half the length of the base's side) and the slanted side of the pyramid ON\text{ON} isolate the angle γ\gamma (OP^N\text{O}\widehat{\text{P}}\text{N}). We use another right triangle identity to calculate it:

cos⁡γ=PNON → γ=arccos⁡(PNON)\footnotesize \cos{\gamma}=\frac{\text{PN}}{\text{ON}}\ \rightarrow \ \gamma=\arccos{\left(\frac{\text{PN}}{\text{ON}}\right)}

The last angle, δ\delta, can be computed using trigonometry again, or if laziness is allowed, by considering that the sum of the internal angles of a triangle is 180°180\degree.

δ=180°−2×γ\delta = 180\degree - 2\times\gamma

How to calculate the angles of a square pyramid

We will guide you step by step in calculating the angles of a right square pyramid. In fact, not of a general square pyramid - let's calculate the angles of the Great Pyramid of Giza!

The great pyramid of Giza
The Great Pyramid of Giza is a great pyramid in Giza.

We need to take some measurements:

  • The original height of the pyramid is 146.7 m146.7\ \text{m}; and
  • The side measures 230.6 m230.6\ \text{m}.

Let's calculate the segment connecting the midpoint of the side to the center. Since the base is a square, it's value is half the length of the side:

CM=AB2=230.6 m2=115.3 m\footnotesize\text{CM}=\frac{AB}{2}=\frac{230.6 \ \text{m}}{2}=115.3\ \text{m}

We can calculate the angle α\alpha:

α=arctan⁡(OCCM)==arctan⁡(146.7 m115.3 m)=51.83°\begin{align*} \footnotesize\alpha & \footnotesize = \arctan{\left(\frac{\text{OC}}{\text{CM}}\right)} =\\ &\footnotesize=\arctan{\left(\frac{146.7\ \text{m}}{115.3\ \text{m}}\right)} = 51.83\degree \end{align*}

To calculate the angle in the corner of the base, we need the measure of half its diagonal β\beta.

β=arctan⁡(OCAC)==arctan⁡(146.7 m115.3×2 m)=41.98°\begin{align*} \footnotesize\beta & \footnotesize = \arctan{\left(\frac{\text{OC}}{\text{AC}}\right)} =\\ &\footnotesize=\arctan{\left(\frac{146.7\ \text{m}}{115.3\times\sqrt{2}\ \text{m}}\right)} = 41.98\degree \end{align*}

🙋 Ancient Egyptians measured the slope of a right pyramid using the seked, a unit corresponding to the numbers of horizontal cubits corresponding to a rise of one cubit in height. The base angle of the Great Pyramid of Giza has a seked of 5125\tfrac{1}{2} sekeds.

What about the angle on each face?

We can use the formulas above to find the value of γ\gamma and δ\delta; however, we need to calculate the length of the slanted side first:

OB=CO2+AC2=146.72+2×(115.3)2=219.3 m\begin{align*} \footnotesize \text{OB} & \footnotesize =\sqrt{\text{CO}^2+\text{AC}^2} \\ & \footnotesize = \sqrt{146.7^2 + 2\times(115.3)^2}\\ &\footnotesize = 219.3\ \text{m} \end{align*}
The great pyramid of giza
Egyptians and mathematics went hand in hand. However, we are sure that they weren't marking angles with Greek letters!

Let's proceed with the calculations.

γ=arccos⁡(PNON)==arccos⁡(115.3 m219.3 m)=58.29°\begin{align*} \footnotesize\gamma & \footnotesize = \arccos{\left(\frac{\text{PN}}{\text{ON}}\right)} =\\ &\footnotesize=\arccos{\left(\frac{115.3\ \text{m}}{219.3\ \text{m}}\right)}= 58.29\degree \end{align*}

Finally, the angle of a face at the apex of the pyramid, δ\delta, is:

δ=180°−2×γ==180°−116.58=63.42°\begin{align*} \footnotesize\delta & \footnotesize = 180\degree - 2\times\gamma=\\ &\footnotesize = 180\degree-116.58=63.42\degree \end{align*}

How to use our pyramid angle calculator

Our pyramid angle calculator can help you with many types of regular right pyramids. Select the type of base you need; we included:

  • Square;
  • Regular pentagon;
  • Regular hexagon;
  • Regular heptagon; and
  • Regular octagon.

Insert the available measurements in the calculator, and find the results!

🙋 Our tools work in reverse, too. For example, you can insert the value of the base angles and find out the pyramid's height!

Do you want to expand your pyramidal knowledge outside of geometry? Visit our Minecraft's pyramid block calculator!

FAQs

What is the best angle for pyramid power?

Pyramids are surrounded by mysticism and occultism. The truth is that there's no such thing as pyramid power, hidden purposes, and alien involvement. Pyramids, and in particular ancient pyramids, are neat but not mystic! The math behind them, however, is all true!

What is the angle of a hexagonal pyramid with side 2 and height 3?

To calculate the angle at the base of a hexagonal pyramid, follow these steps:

  1. Calculate the length of the segment MC connecting the side's midpoint to the centroid.
  2. Apply the inverse tangent function to the ratio of the height and the length just calculated: OC/MC.

For a hexagon with side 2 and height 3, it means:

  • MC = 2 × cos(30°) = 2 × (sqrt(3)/2) = sqrt(3)
  • α = arctan(3/sqrt(3)) = arctan(sqrt(3)) = 60°

How do I calculate the angles at the base of a square pyramid?

To calculate the angles at the base of a pyramid, you can use the trigonometric formulas of right triangles. Calling the height h and the side L, the value of the base angle is:
α = arctan(h/(L/2))
We calculate the angle in the corner of the base using half the diagonal:
ß = arctan(h/(sqrt(2) × L/2)) = arctan(h/(L/sqrt(2)))

What are the angles of the Great Pyramid of Giza?

The Great Pyramid of Giza has a base angle of 51.83°. We can calculate it using the inverse trigonometric function arctangent, knowing the height and the side of the pyramid:
α = arctan(146.7/115.3) = 51.83°
The angle in the corner of the base is slightly smaller: 41.98°.

VPD Calculator & Chart (Vapor Pressure Deficit)Sod CalculatorMolar Mass CalculatorLeast Common Multiple CalculatorAbsolute Value CalculatorInterval Notation CalculatorLeast Common Denominator CalculatorNull Space CalculatorTrig Identities CalculatorPartial Fraction Decomposition CalculatorUnit Rate CalculatorExponential Function Calculator
pyramid

Base and measurements

Check out 23 similar 3d geometry calculators 📦
Area of a hemisphereCubeCube Calc: find v, a, d...20 more