Triangular Pyramid Volume Calculator

Our triangular pyramid volume calculator allows you to find the volume of any pyramid with a triangular base, regardless of whether or not you know the area of its base. If you want to determine the volume of a right triangular pyramid or a regular tetrahedron, you've come to the right place.
Do you need to learn how to find the volume of a triangular pyramid by hand? Keep reading as we give both the formula as well as examples of how to use it.

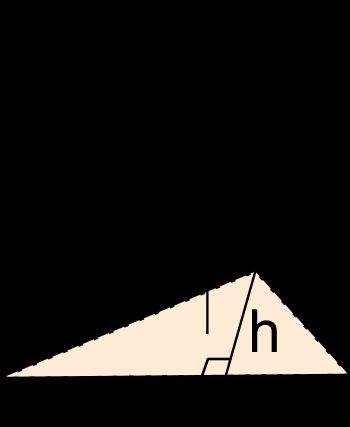
A triangular pyramid is a solid object formed by connecting a triangular base to a point, called the apex. This creates four faces, each of which is a triangle. If you can rotate the pyramid, each face can play the role of the pyramid's base. The segment that is perpendicular to the base and runs through the apex is known as the height of the pyramid.

Here the dark blue triangle is the base of the pyramid, and the dotted black segment is the height:

To use our triangular pyramid volume calculator, follow these steps:

1. Do you know the area of the pyramid's base?

• If so, enter it into the calculator.
• If not, check what data about the base you do know: choose the appropriate option in our calculator and enter your data. The base area will be calculated for you.

2. Enter the pyramid's height.

3. The triangular pyramid volume calculator will then return your pyramid's volume :)

The triangular pyramid volume formula is:

V = A × H / 3,

where:

• V is the triangular pyramid volume;
• A is the area of the pyramid's base; and
• H is the height from the base to the apex.

In words: the volume of a triangular pyramid is one-third of the product of the base area and the pyramid's height.

To find the volume of a triangular pyramid with a height of 10 cm, and a right-triangle base with sides 3 cm, 4 cm, and 5 cm, you need to:

1. Determine the area of the base: for us, it's 3 × 4 / 2 = 6.
2. Find the pyramid's height: in our case, it's 10.
3. Apply the triangular pyramid volume formula: 6 × 10 / 3 = 20.
4. The volume is 20 cm³.

The hardest step is usually calculating the base area - to learn more about it, you may want to check our generic triangle area calculator or one of the calculators dedicated to each special type of triangle, be it:

• Equilateral triangle calculator;
• Isosceles triangle calculator; or
• Area of a right triangle calculator.

If you need to know how to find the volume of a triangular pyramid that is a regular tetrahedron, or a right triangular pyramid, then check out the two remaining sections where we give the appropriate formulae.

A triangular pyramid that has equilateral triangles as its faces is called a regular tetrahedron.

The volume of a tetrahedron with side of length a can be expressed as:

V = a³ × √2 / 12,

which is approximately equal to V = 0.12 × a³.

For instance, the volume of a tetrahedron of side 10 cm is equal to

V = 6³ × √2 / 12 = 18 √2,

which can be approximated as 0.12 × 6³ = 25.92.

A pyramid is right if its apex is directly above the centroid of the base. Otherwise, the pyramid is called oblique. If, additionally, the base is an equilateral triangle, then the following formulae for volume hold:

• If the base has sides of length a and the pyramid height is H, then:

  V = a² × H × √3 / 12

• If the base has sides of length a and the edges between the base and the apex have length b, with the help of the Pythagorean theorem, we can find the height of the pyramid and then the volume:

  V = √(b² - a²/3) × a² × √3 / 12

To determine the side of a tetrahedron from its volume:

1. Multiply the volume by 12.
2. Divide the result by √2 ≈ 1.41.
3. Take the cube root.
4. That's it! You've found the side of your tetrahedron.

The answer is 1.6654 × ∛Volume. We get this result by merging the formulas: Height = √(2/3) × Side and Volume = a³ × √2 / 12, which results in the formula Height = √(∛576 / 3) × ∛Volume. Approximately, we get Height ≈ 1.6654 × ∛Volume, as claimed.