Right Rectangular Pyramid Calc: find A, V, A_l, A_b

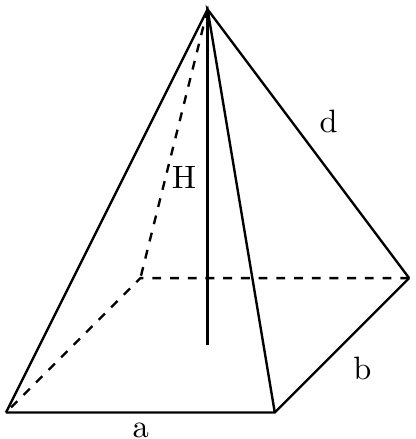
Greetings adventurer, to the right rectangular pyramid calculator. Today we will learn how to find the volume of a rectangular pyramid. As the name suggests, we will be dealing with pyramids that have rectangles as their bases, while the "right" part means that the apex is directly above the center of the base. We will use the following notation:

• V – Volume of the pyramid;
• A – Total surface area of the pyramid;
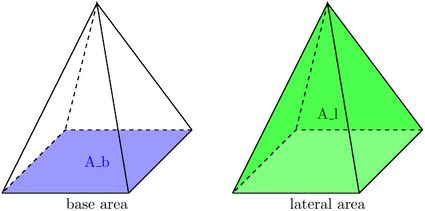
• A_l – Lateral surface area;
• A_b – Base area; and
• H – Pyramid height.

In other words, our right rectangular pyramid calc will find V, A, A_l, and A_b for no matter the pyramid's base and height. Remember that every square is a rectangle (but the opposite is not true!), so this calculator can also deal with problems related to right square pyramids, such as, e.g., how to find the surface area of a square pyramid. However, you may also want to take a look at our dedicated right square pyramid calculator. Ready to begin your quest for knowledge? I know I am!

Let's begin with a question that may have bugged you for years: what is the volume of the Great Pyramid of Giza? Unfortunately, "probably a lot" is often not a sufficient answer, so let's take a look at the square pyramid volume formula to see what we're dealing with:

volume = (base_area × pyramid_height) / 3.

Note that we will need to know the base area. As you may know, the Great Pyramid of Giza's base is a square, so we will use the well-known formula of area = a × a, where a is the base side length. If you happen to be an ancient Egyptian, this is equal to 440 Egyptian Royal cubits. (Also, in this case, please let us know how you do that pose that is on all your hieroglyphs because some of us have been trying to bend our hands that way since primary school, and we just can't get it right.) Otherwise, let's use the good old metric system – 230 meters. Moreover, we will need the height of the pyramid, so once again, we use our favorite search engine and find that it is 147 meters (or 280 Egyptian Royal cubits). Now we're left with the most fun part, counting! Yay, right? Right...?

Using the above square pyramid volume formula, we find that:

volume = ((230 × 230) × 147) / 3 = 2,592,100 m³,

or roughly 3,390,339 cubic yards if you prefer imperial. It seems that we weren't so far from the actual answer with our initial "probably a lot."

Observe that when we asked ourselves how to find the volume of a rectangular pyramid above, we had to know the base area of the pyramid, i.e., the value A_b. Let us now take care of the other faces of the pyramid and find the lateral area, A_l.

At first glance, you might think that we might have a problem here since the lateral edges are triangles, whose surface area formula is area = (a × h) / 2, where a is the base length and h is the height projected onto that a, also called the slant of the pyramid. We usually know a well enough, but h can get a little tricky. But worry not, my friend! As long as we know a and the pyramid height, we can calculate h using the Pythagorean theorem.

This way, we arrive at the not-so-scary-anymore formula:

A_l = A₁ + A₂ + A₃ + A₄,

where the indexed A-s denotes the surface area of consecutive lateral faces. A scrupulous eye will notice that, in fact, among the four, we have two pairs of equal areas, and if the base is a square, all four of them are equal.

We've seen how to find the lateral surface area, so let's now see how our right rectangular pyramid calc will find A_b and A, i.e., the base area and total surface area, respectively.

We've already seen in the example above how to find the base area of a square. The general formula for the base of a rectangular based pyramid is just as easy:

base_area = a × b,

where a and b denote the lengths of the sides of the base. The last step in our considerations is given by:

total_surface_area = base_area + lateral_surface_area,

or A = A_b + A_l for short, with the notation we introduced earlier.

Okay, let's now get down to details and see our calculator in action. Suppose we know how to find the volume of a rectangular pyramid. Say that its base is 6 by 8 inches, and its height is 12 inches. We'll try to follow the way the calculator thinks, and see how it arrives at the answer.

Using the notation in the calculator and on the picture, we have a = 6 in and b = 8 in. From the formula in the above section, we find that:

A_b = a × b = 6 × 8 = 48 in².

Now that we know the area of our base, we can use the volume formula from the first section to calculate that:

volume = (48 × 12) / 3 = 192 in³.

Great, we have what we came for! But let's try to dig deeper and get some more information. Now that we've found the volume of the pyramid let's try to find its surface area. Although in the beginning we were given only three values, it turns out that they are just enough to know everything about the pyramid.

Before going further, note that while the right rectangular pyramid calculator counts all of the numbers, we will now mention that some of them are hidden in the further properties section.

Base diagonal: The diagonal of the rectangle that forms the base of our pyramid has sides a and b. Therefore, we can calculate its length using the already-mentioned Pythagorean theorem:

diagonal² = a² + b² = 6² + 8² = 100,

and hence diagonal = 10 in.

Lateral edge: Since we've calculated the base diagonal, let's now use it to count the length of the lateral edge, d. To do this, observe that it forms a right triangle with the pyramid's height and half of the base diagonal. Therefore, the Pythagoras theorem comes in handy again:

d² = H² + (diagonal / 2)² = 12² + 5² = 169,

which gives d = 13 in.

Slant height: The slant height is the height of one of the triangular faces that make up our pyramid. Therefore, it must form a right triangle with the lateral edge and half of a base side. Yes, you guessed it – Pythagoras the Useful makes an appearance again. Note, however, that this time we want to study one of the sides that forms the right angle, so the calculations differ slightly from what we've used before. Let us try to find the slant height where the base side has length a:

slant_height_onto_a² = d² - (a / 2)² = 13² - 3² = 160,

and hence slant_height_onto_a = 4√10 ≈ 13.342 in. Similar calculations with a exchanged for b give slant_height_onto_b ≈ 13.601 in. Lastly, observe that when the base of our pyramid is a square, the two slant heights are equal, so the calculator will show that value only once.

Lateral face area: Recall from the second section that the formula for the area of a triangle is area = (a × h) / 2. It seems that we've acquired all the information we needed to calculate the area of the pyramid's lateral face. Indeed, we get the following:

lateral_face_area_over_a = (a × slant_height_onto_a) / 2 ≈ (6 × 13.342) / 2 = 40.025 in².

Once again, by exchanging a for b in the above formula, we get lateral_face_area_over_b ≈ 54.41 in². Also, similarly to before, if the base of the pyramid is a square, the two values are equal, so the calculator will show the number only once.

Lateral surface area: Now that we've calculated all of the lateral faces, we need to use the formula from section 2:

A_l = 2 × lateral_face_area_over_a + 2 × lateral_face_area_over_b ≈ 188.86 in².

Total surface area: The last step in our calculations is arguably the easiest one. Now that we know the areas of all the pyramid's faces, we just plug the values in the formula for A to obtain:
A = A_b + A_l ≈ 236.86 in².

While pharaohs had been pretty consistent with what shape they wanted their tombs to be, textbooks and general life problems are not so considerate. So what if the base is something else, e.g., a circle or a triangle? The interesting thing is that the square pyramid volume formula we introduced in the first section still works. How so? Well, let's recall that it stated that:

V = (A_b × pyramid_height) / 3.

There is no saying what shape the base is. We can have the most funny-looking shape that you can imagine, and it will still work. Verify that with Omni's triangular pyramid volume calculator or cone volume calculator!

Note, however, that when we're dealing with prisms instead of pyramids, the volume formula looks exactly the same as above, but without the division by 3. Go to, for instance, Omni's rectangular prism calculator to see how this works.