Right Square Pyramid Calc: find A, A_l, V, A_F
In this right square pyramid calculator, you'll be able to learn:
- how to find the volume of a right square pyramid,
- how to calculate the surface area of a right square pyramid, and
- the different formulas for right square pyramids.
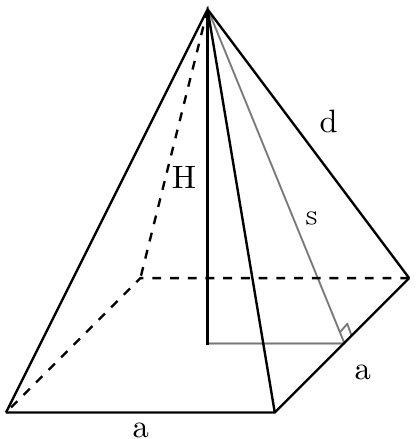
What's even great is you can find all of them by just knowing any two of your pyramid's dimensions: base edge (a), pyramid's height (H), slant height (s), or lateral edge (d), as shown in the image below:
Have you got a project concerning the right square pyramids? Do you want to learn the different formulas for right square pyramid calculations? Then this right square pyramid calculator is for you! 🙂
If you're ready to use our right square pyramid calc to find:
A_f- lateral face area,A_l- total lateral area,A- total surface area, andV- volume,
then keep on reading 🙂
How to use the right square pyramid calculator
Using this right square pyramid calc to find A, A_l, A_f, or V, is very easy, and you only need any two known dimensions of your right square pyramid to find anything you need!
By entering values for base edge a length and pyramid height H, you can instantly find your pyramid's other dimensions, i.e., slant height s and lateral edge d length, or vice versa. You can also input values for a and d to get H and s. You get the point. After entering at least two dimensions, this right square pyramid calc finds volume V and total surface area A, together with the other surface areas of your pyramid, all at the same time.
In the advanced mode of this calculator, you'll find that you can also enter a value for the base diagonal length together as another dimension to see the final results. We have a separate diagonal of a square calculator if you want to learn more about that 🙂.
If you're curious to learn the right square pyramid formulas that we use in this calculator, you'll learn them all in the following sections of this text. Read on to continue learning how to calculate the total surface area of a right square pyramid and its volume.
What a right square pyramid is and how to find A_l
When talking about pyramids, square pyramids are by far the most common pyramid that we can maybe think of first. You may have already heard of and seen pictures of the Great Pyramids at Giza. That is an example of a right square pyramid (at least approximately).
We call a square pyramid "right" (or "regular") whenever its vertex coincides directly on top of the center of its square base (hence the name "square" pyramid). The term "right" came from the right angle formed by an imaginary line connecting the center of the pyramid's square base and the pyramid's vertex. This characteristic of a right square pyramid results in its lateral faces being equal. We can also observe this with other right pyramids with regular polygon bases.
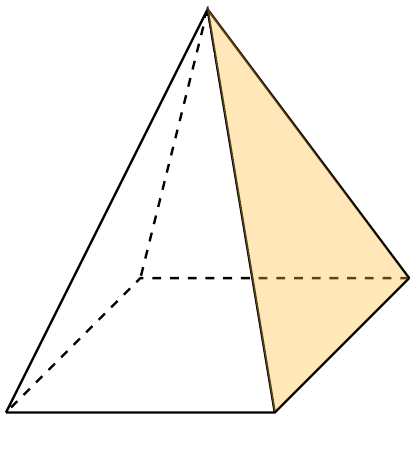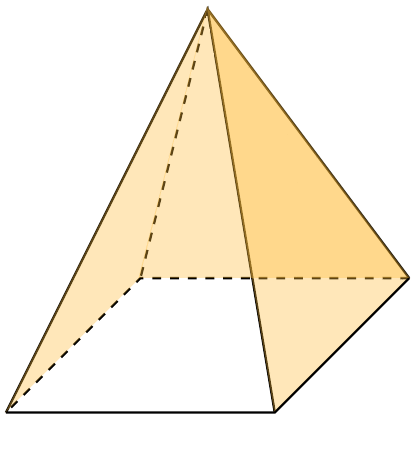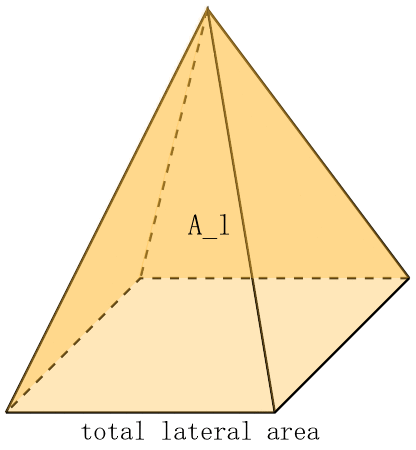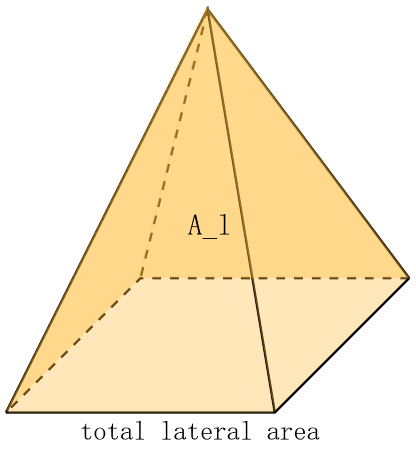
With that said, when determining the total lateral area of a right square pyramid (shown in the animated image above), we denote as A_l, we can calculate it by finding the lateral face area, A_f, and multiplying it by 4, as shown in the equation below:
A_l = 4 * A_f
💡 The total lateral area is what we need; let's say if we want to paint the visible sides of a pyramid.
Right square pyramid calc: Find A_f
Since we cannot find A_l without knowing A_f (shown in the image below), in this section, we'll discuss how to calculate A_f.
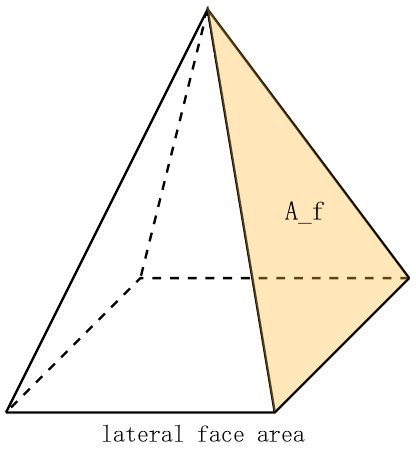
To find A_f, we consider one lateral face of the pyramid, which is an isosceles triangle, and calculate its area using this formula:
A_f = (a * s) / 2
where:
a- The side measurement of the pyramid's square base; ands- The slant height of the pyramid.
The slant height is also the hypotenuse of an internal imaginary right triangle (highlighted with pink) formed inside the pyramid as shown in the image below:
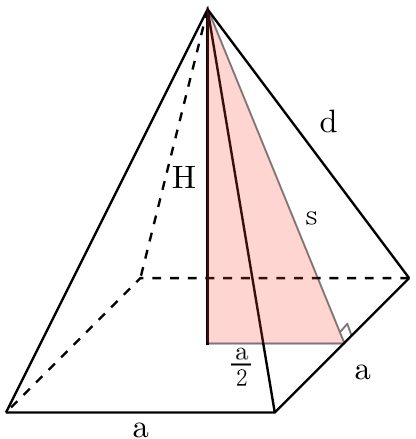
With the help of the Pythagorean Theorem, we can find the slant height using this formula:
s² = H² + (a / 2)²,
where H is the height of the square pyramid.
💡 While we're here, we can also find the lateral edge, d, by considering the right triangle formed by dividing the lateral face in half and using the Pythagorean Theorem like this:
d² = s² + (a / 2)²
By expressing the slant height in terms of H and a, we can have a simplified formula in finding d as shown below:
d² = H² + a² / 2
We can also find the height of a right square pyramid, H, by measuring its lateral edge (d) and reorganizing the formula above to form this equation:
H² = d² - a² / 2
🙋 Contrary to what we discussed earlier, in reality, we can find A_l without A_f. But only if we know s. So now, if we substitute the formula of A_f into the A_l formula, and simplify it, we can get this simpler equation for A_l:
A_l = 2 * a * s
Total surface area of a right square pyramid
Going back to the surface area of a right square pyramid, if we want to calculate its total surface area, A, we need to add the base area, A_b, to the lateral surface area, A_l as shown below:
A = A_l + A_b
Since we're dealing with a pyramid with a square base, its base area will simply be the area of a square which will be equal to:
A_b = a²,
where a, again, is the side measurement of the square-shaped base of the pyramid.
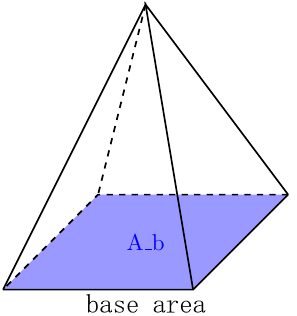
The base area of the right square pyramid is not only for finding the total surface area of your pyramid. You will also definitely use the base area in finding the volume of your pyramid. Learn how to do it in the next section of this text 🙂
Formula for the right square pyramid volume
Finding the volume of a right square pyramid follows the same concept as finding the volume of a cone. Multiplying the pyramid's base area by the pyramid's height and dividing it by 3, we get the volume of our solid as shown in this equation:
V = A_b * H / 3
🔎 Since a square is also technically a rectangle (but not vice versa), you can also use our right rectangular pyramid calculator in obtaining the results in this calculator. However, you will have to input the measurement of the base twice there.
Knowing how to calculate the volume of a right square pyramid can be very helpful for, let's say, molding and casting projects. To quantify how much to pour in a right square pyramid-shaped mold, you can then easily calculate your mold's volume after measuring, say, the inner side measurement of your mold (a), and perhaps the height (H) or lateral edge (d).
Other related calculators
If you find this calculator informative and interesting, perhaps you'll find these useful, too:
FAQ
What is the volume of a right square pyramid that can fit in a 12-inch cube?
Since our right square pyramid fits in a 12-in cube, our pyramid's base edge measures 12 inches, and its height is 12 inches. To get its volume:
- Obtain the base area by squaring the base edge length, 12 in * 12 in = 144 in².
- Next, multiply this area to the pyramid's height, 144 in² * 12 in = 1728 in³.
- Finally, divide this by 3, 1728 in³ / 3 = 576 in³.
What is the surface area of a right square pyramid?
Let's say its base measures 6 inches, its height 4 inches, and its slant height 5 inches:
- First calculate its lateral face area, 6 in * 5 in / 2 = 15 in².
- After that, multiply the lateral face area by 4 to find the total lateral area (A_l), 15 in² * 4 = 60 in².
- Then, find the pyramid's base area (A_b), 6 in * 6 in = 36 in².
- Lastly, add the A_l and A_b to obtain the total surface area, 60 in² + 36 in² = 96 in²
How many right angles does a square based pyramid have?
A right square pyramid only has four right angles and you can find them in the four corners of its square base. All the other angles on a right square pyramid are acute. However, other square pyramids that are not "right" can have one up to 3 (very special case) more right angles on them.
