Cosecant Calculator

Welcome to Omni's cosecant calculator, where we'll study the mysterious csc trig function. Arguably, even if you've had a course in trigonometry (see trigonometry calculator), you may have missed this one since we rarely use it. Nevertheless, the csc in math is a well-defined function that can still appear in some textbooks. Therefore, we've prepared this fantastic tool and article to answer whoever asked the question, "What is csc?". And we'll show you the cosecant formula and cosecant graph to go with it.

So since time is money, let's jump right into the topic!

Geometry begins with the simplest object - the triangle. Once we get the hang of how to calculate their area or perimeter, we move on to more complicated shapes: rhombus, circle, prisms, etc. (cf. surface area calculator).

But let's slow down a little and look back at the starting point. Do we really know triangles that well? Sure, we can write down the formula for the area (if you're feeling particularly brainy today, you can even use Heron's formula). But is there more to those objects? Can we say something more about the sides or angles?

The idea behind trigonometry is to somehow relate the size of a triangle's inside angles to its sides. To get a firmer grip on how it's done, we'll focus on right triangles (you know, the ones that the Pythagorean theorem is about). There, we can easily imagine that if we take one of the acute angles and try to make it larger, then the opposite triangle side will have to be longer too.

We define trigonometric functions as ratios of a triangle's sides. Below, please find a simple picture of a right triangle together with all the formulas (including that of the csc trig function).

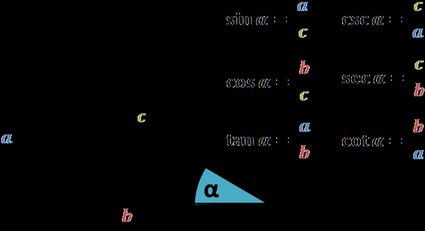
So what is the cosecant? Looking back at the figure above, we see that it's the hypotenuse divided by the side (or leg) opposite the angle. Note that the above definitions do not mention how big the triangle is. In fact, that's where a crucial strength of trigonometry lies: even if we scale the triangle to twice its size, the values of the functions (csc x among them) will not change.

However, there is a price to pay. From the above picture, sin, cos, or csc have a meaning for angles between 0 and 90 degrees (or between 0 and π/2 in radians) simply because it's a right triangle. But... do we really have to pay this price?

As a matter of fact, we don't. There is a way to translate the whole reasoning to take any real number as the angle, even a negative one. The trick is to switch from triangles to the two-dimensional Euclidean space, i.e., the plane.

Let A = (x,y) be a point on the plane, and denote by α the angle going from the positive half of the horizontal axis to the line segment between 0 and A counterclockwise. (Observe how we said that α goes from one line to the other and not that it is between them. Because of that, we often call α a directed angle.)

Clearly, such α can be larger than 90 degrees. Even better - it can go beyond the full angle of 360 degrees! In that case, we just consider the 360 to be a full lap around (0,0), and from that, we begin the second one. And even better! Since we've defined α to be directed, we can now have negative angles. For those, we simply reverse the direction, i.e., go clockwise instead of counterclockwise.

Now that we understand all possible angles let's decipher the csc meaning (and all the other functions', in fact) for them. The rule is simple enough: we recall the notation for the point A = (x,y) and repeat the above formulas by substituting a for y, b for x, and c for √(x² + y²), i.e., the distance between (0,0) and A.

So what is the cosecant in this new notation? According to the above instructions, we get the new csc formula to be

Great, we've learned what csc in math is, or, more precisely, csc in trigonometry. Now it's time to take this cosecant formula, and try to understand and befriend it. For that, we'll draw its portrait - the cosecant graph.

It's quite possible that you've already seen the cosine graph or the tangent graph since they're among the most common trigonometric functions. But csc x is not, so you might have missed that one. And it is a pity since it's quite funny-looking.

So without further ado, here's the cosecant graph in all its glory. (Observe that we use the same picture in our csc calculator.)

From this picture alone, we can deduce quite a few interesting and important properties. For simplicity and for care of your eyesight, we put them in a pretty bullet list.

• Similarly to the secant, csc in trigonometry can either be smaller or equal to -1, or larger or equal to 1. In other words, it admits all real values except for the ones in the (open) interval (-1,1).
• The csc in math language is odd. This means that at x, it admits the opposite value to the one at -x. In symbolic notation, this translates to csc(x) = -csc(-x).
• The csc trig function is periodic with a 360-degree period. This property means that the function's values repeat every 360 degrees. In mathematical language, we can write this fact as sec(x) = sec(x + 360°).
• The cosecant formula is not defined everywhere. For angles of the form x = k·180° for k an integer, there is no csc x. These are precisely the points in which the cosecant graph goes to plus/minus infinity.

We'll take the opportunity to speak some more about the last property above. The csc trig function is undefined at some points (for instance, cot 0 doesn't exist) because of the way it is defined: by a fraction.

We know all too well that we can never divide by zero, and the undefined points, i.e., x-s of the form x = k·180° for k an integer, are precisely those where this would potentially happen (for instance, for k = 0, we have csc 0). As such, they do not belong to the csc x domain, that is, the set where the map is defined. If we were to please a few big-headed mathematicians, we could write this whole paragraph symbolically like this:

where D(csc) denotes the domain of the csc trig function.

And with that, we proclaim the end of this section. Two are done, two more to go! The next one is going to be slightly more algebraic because we'll try to find an answer to "What is csc?" that uses functions and operations rather than words. So if you feel like you need a coffee kick beforehand, then now's the time to have it. If not, let's get to it!

When we begin studying trigonometry, we first learn the definitions (e.g., how the csc formula is the ratio of two sides). The next step is to leave the triangle and the two-dimensional coordinates aside, and try to relate one function to some of the others to obtain so-called trigonometric identities. Just to give you a taste of how useful those can be, let us direct you to two examples: the law of sines and the law of cosines.

In essence, we'll try to make the formula for csc from trigonometry work in our favor by playing around with it. For instance, recall from the first section how to find the csc function: we divide the length of a right triangle's hypotenuse by the side opposite the angle. Observe that we use the same lengths in the definition of the sine. The only difference is that there, they are reversed.

Therefore, we obtain our first alternative cosecant formula:

Or, if you prefer fractions,

However, note that this does not mean that csc x is the inverse function of sin x. That would be arcsin, which takes the sine function's value and returns the angle that corresponds to it. Here, on the other hand, the -1 in the exponent means only that csc x is the inverse of sin x (not the inverse function; those two are quite different things).

Next, if we take this new csc meaning and recall a simple trigonometric identity for the cotangent (i.e., that cot(x) = cos(x) / sin(x)), then we can get another interesting cosecant formula.

With that, we now have four different answers to the "What is the cosecant?" question. Observe that each has some expression in the denominator, which, obviously, cannot be zero. Those are the points we mentioned in the previous section where our function is undefined (e.g., when we have csc 0).

We hope that you begin to feel more comfortable around the cosecant function after all that we've learned about it today. If so, it's time to see how to find the csc in practice.

In other words, we move to examples.

The clock is ticking, and it's time to think about choosing the college (or colleges) that you want to apply to. But first, it'd be best to get a grip on what area you want to focus on.

To get a feel of it, you decide to take a look at a test example in trigonometry. After all, college mathematics can't be that hard, can it?

The first question is to calculate the cosecant of the following angles: 30°, 45°, 60°, and 75°. Oh, what a coincidence! It's as if they've made the exercise to accompany the article we're reading!

We begin by appreciating how easy the task is when we have Omni's cosecant calculator at hand. In there, we only have one variable field: the angle. We input the values that the question gives us one by one, and the tool spits out the answer underneath. Note how for 45° and 60°, we also obtain a precise value before rounding it up, i.e., with simple fractions and square roots. We'll explain why it is so in a minute.

Now, let's leave the cosecant calculator aside and see how to find the csc values ourselves. We'll use the right triangle definition from the first section, but feel free to try out any other cosecant formulas.

First of all, we'll draw an example triangle for each of the angles given. We begin with the one for 30°.

Note that this is an example of quite a special right triangle in which we know the relations between the sides. For instance, we know that if the shorter leg is of length x, then the hypotenuse must be 2x. This is because our shape is, in fact, half of an equilateral triangle. Also, note how the triangle's other angle is 60°, so we can use the same picture for that case as well.

The csc formula in the first section states that the cosecant is the ratio of the hypotenuse to the side opposite the angle. In our triangle, this gives

Next, we move on to the 45° case.

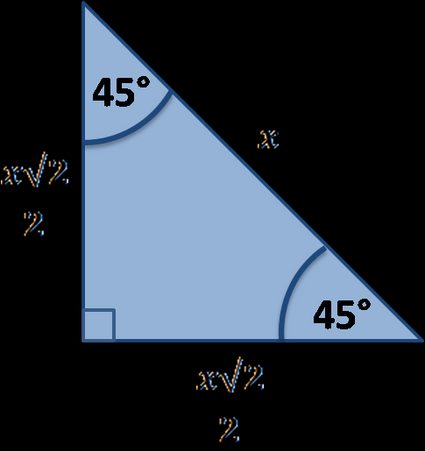
Again, we're fortunate enough to know the relations between the sides. This time, it is because our triangle is half of a square, with the hypotenuse being the diagonal.

We obtain:

Lastly, we have the 75° angle. However, here the story is not that simple: we have no special triangle upon which to base our calculations.

What we could do is use the alternative formula from the above section with the sine. This, in turn, would require us to find sin(75°). For that, we can use the half-angle formulas and sin(150°), which is, in fact, not that difficult to calculate since 150° = 180° - 30°, and both 180° and 30° are fairly simple angles.

What we learn here is that, as it turns out, calculating trigonometric functions is, in general, no walk in the park. Most of the time, we use external tools for it, like Omni's cosecant calculator.

Nevertheless, we got three out of four angles fairly easily, and the last one would require some work, but is perfectly doable. Maybe trigonometry in college wouldn't be that bad? Maybe math is the way to go? After all, the branch surely has some good perspectives and decent salaries to go with them.