Surface Area Calculator

This surface area calculator helps you find the area of the most common three-dimensional solids. If you have ever wondered how to find a surface area or what is the lateral surface area, this calculator is here to help you. Surface area has a gigantic list of applications in every field, such as aerodynamics.

In this article, you can find the formulas for the surface area of a sphere, cube, cylinder, cone, pyramid, and rectangular/triangular prism. We will also explain how to calculate the surface area of a sphere as an example.

Surface area is the total area that the surface of the object occupies. In other words, it's the total area of the surface of a 3D object.

Sometimes the surface area may be split into a sum of base area(s) and lateral surface area. The lateral surface is the area of all the sides of the object, excluding its base and top. This division is used for shapes where there is an obvious distinction between the base and the other part – e.g., for a cylinder, cone, pyramid, or triangular prism. It's rarely applied to solids for which we are not sure which faces should be treated as bases (like in a cube or box), and we don't use it for smooth surfaces such as a sphere.

Our surface area calculator can find the surface area of seven different solids. The formula depends on the type of solid.

• Surface area of a sphere: A = 4πr², where r stands for the radius of the sphere.

• Surface area of a cube: A = 6a², where a is the side length.

• Surface area of a cylinder: A = 2πr² + 2πrh, where r is the radius and h is the height of the cylinder.

• Surface area of a cone: A = πr² + πr√(r² + h²), where r is the radius and h is the height of the cone.

• Surface area of a rectangular prism (box): A = 2(ab + bc + ac), where a, b and c are the lengths of three sides of the cuboid.

• Surface area of a triangular prism: A = 0.5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c)) + h × (a + b + c), where a, b and c are the lengths of three sides of the triangular prism base and h is a height (length) of the prism.

• Surface area of a pyramid: A = l × √(l² + 4 × h²) + l², where l is a side length of the square base and h is a height of a pyramid.

But where do those formulas come from? How to find the surface area of the basic 3D shapes? Keep reading, and you'll find out!

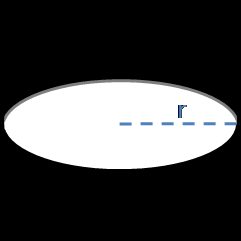
To calculate the surface area of a sphere, all you need to know is the sphere's radius - or its diameter.

• A = 4 × π × r² where r is the radius.

As we know that the diameter of a sphere is equal to two radii d = 2r, we can transform the equation into another form:

• A = 4 × π × (d / 2)² = π × d² where d is the sphere diameter.

The derivation of this surface area formula requires integration. If you're curious, check out this proof.

To find out the surface area of a cylinder, you should have two values: the radius (or diameter) of a base and the height of the cylinder. The general equation is as usual - base areas plus lateral surface area. In our case, a circle is a base.

• A = 2πr² + 2πrh

Where does this formula come from? You can write the equation for the surface area of a cylinder as:

• A = A(lateral) + 2 × A(base)

It's easy to find a base area - we remember the well-known formula for the area of a circle: A(base) = π × r². But what's the shape of the lateral surface area? Try to imagine that we "unfold" it. Do you recognize it? It's a rectangle! One side length is a cylinder height, and the second one is the unfolded circle circumference.

• A(base) = π × r²
• A(lateral) = h × (2 × π × r)

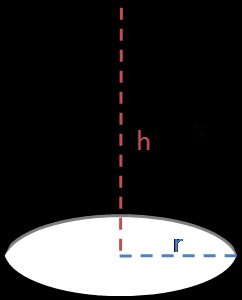
We may split the surface area of a cone into two parts:

• A = A(lateral) + A(base), as we have only one base, in contrast to a cylinder.

The base is again the area of a circle A(base) = π × r², but the lateral surface area origins maybe not so obvious:

• A(lateral) = π × r × √(r² + h²)

Let's have a look at this step-by-step derivation:

1. Roll the lateral surface out flat. It's a circular sector, which is the part of a circle with radius s (s is the cone's slant height).

2. For the circle with radius s, the circumference is equal to 2 × π × s. The arc length of the sector is equal to 2 × π × r.

3. The area of a sector - which is our lateral surface of a cone - is given by the formula:

• A(lateral) = (s × (arc length)) / 2 = (s × 2 × π × r) / 2 = π × r × s

  The formula can be obtained from proportions, as the ratio of the areas of the shapes is the same as the ratio of the arc length to the circumference:

  (sector area) / (large circle area) = (arc length) / (large circle circumference) so:

  (sector area) / (π × s²) = (2 × π × r) / (2 × π × s)

  (sector area) = (π × s²) × (2 × π × r) / (2 × π × s)

• A(lateral) = π × r × s

  For finding the missing term of this ratio, you can try out our ratio calculator, too!

4. Usually, we don't have the s value given but h, which is the cone's height. But that's not a problem at all! We can easily transform the formula using Pythagorean theorem:

• r² + h²= s² so taking the square root we got s = √(r² + h²)

  Thus, the lateral surface area formula looks as follows:

• A(lateral) = π × r × √(r² + h²)

5. Finally, add the areas of the base and the lateral part to find the final formula for the surface area of a cone:

• A = A(lateral) + A(base) = π × r × s + π × r² given r and s or
• A = π × r × √(r² + h²) + π × r² given r and h.

The surface area of a cube is the easiest you can imagine: each of the sides is a square! As every cube has six identical square faces, the surface area equals:

• A = 6 × (side area)

As the area of a square is the product of the length of its sides, the final formula for the surface area of a cube is:

• A = 6 × l², where l is a square side

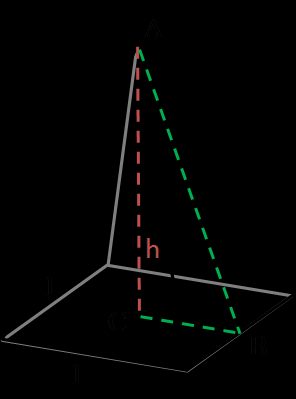
A pyramid is a 3D solid with a polygonal base and triangular lateral faces. When you hear a pyramid, it's usually assumed to be a regular square pyramid. But depending on the shape of the base, it could also be a hexagonal pyramid or a rectangular pyramid one. Regular means that it has a regular polygon base and is a right pyramid (apex directly above the centroid of its base), and square – means that it has this shape as a base. That's the option that we used as a pyramid in this surface area calculator.

The formula for the surface area of a pyramid is:

• A = l × √(l² + 4 × h²) + l² where l is a base side, and h is a height of a pyramid

Again, we can split the equation into:

A = A(base) + A(lateral) = A(base) + 4 × A(lateral face)

The base is in the shape of a square, so A(base) = l². To calculate the lateral surface area, let's start with the area of one triangular face:

1. To find the height of the triangle, we will need the formula for hypotenuse again:

   c = √(a² + b²)

2. Calculate the triangle ABC hypotenuse (which is at the same time the height of the triangular face):

   c = √(h² + (l/2)²) = √(h² + l²/4)

3. The area of a triangle (in our case, it's an isosceles triangle) may be calculated as:

   A = height × base / 2 so

   A(lateral face) = √(h² + l²/4) × l / 2

4. So the final formula for the surface area of a pyramid is:

   A = l² + 4 × √(h² + l²/4) × l / 2 = l² + 2 × l × √(h² + l²/4)

   A = l² + l × √(4 × h² + l²)

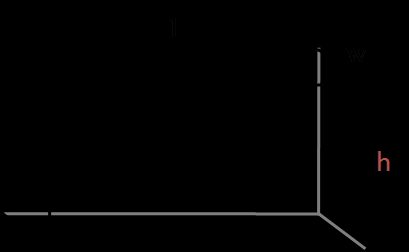
To calculate the surface area of a rectangular prism, all you need to do is to calculate the areas of the rectangular sides:

• A = 2 × (A1 + A2 + A3)

where:

• A1 = l × w
• A2 = w × h
• A3 = l × h

Thus, the final formula is:

• A = 2 × (l × w + w × h + l × h)

To understand where the formula for the surface area of a triangular prism comes from, let's have a look at this derivation:

1. The lateral surface area part is easy to calculate in this case. As you can see from the picture, it consists of three rectangles, with one side length in common:

   A(lateral) = a × h + b × h + c × h = h × (a + b + c)

   which we can also write in short as:

   A(lateral) = h × P, where P is the perimeter of one of the base triangles

2. Then, find the area of one of the triangular bases. You can do it in many ways, depending on what you are given. In our calculator, we've implemented the calculation based on Heron's formula - it's used when you have three triangle sides given (SSS).

   A(base) = 0.25 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

3. The final formula for a surface area of a triangular prism:

   A = A(lateral) + 2 × A(base)

   A = h × (a + b + c) + 0.5 × √((a + b + c) × (-a + b + c) × (a - b + c) × (a + b - c))

You can calculate the surface of any solid, for example, your body - it doesn't need to be the simple shape from geometry! If you're curious what's the external surface area of a human body, check out this body surface area calculator.

If you want to find the surface area of a sphere, you need to follow these steps:

1. Determine the radius of the sphere. We can assume a radius of 10 cm.

2. Input this value into the formula:

   A = 4πr²

3. Calculate the result:

   A = 4π × 10² = 1256 cm²

4. You can also use an online surface area calculator to find the sphere's radius if you know its area.

The units of surface area are always square units of length. For example, you can express it in cm², in², ft², m², but also in acres and hectares.

If you want to find the volume of any of these solids, use our volume calculator to do it.

To convert the surface area of a cube to the length of its side, follow these steps:

1. Write down the area of your cube.
2. Divide it by six. The result is the area of one face.
3. Take the square root of the number from Step 2.
4. This is the length of each side of your cube. Well done!

To deduce the radius of a sphere from its surface area:

1. Write down the surface area of the sphere.
2. Divide it by 4π ≈ 12.566.
3. Take the square root: √(Area / 4π).
4. That's it; this is the radius! You can verify your result using an online surface area calculator.

The answer is 50.2655 in sq. To derive this result, recall that the surface area formula of a cylinder is:

Area = 2πr(r + h)

Plugging in r = h = 2, we obtain Area = 16π ≈ 50.2655. Remember the units! Since both r and h are in in, the area is in in sq.