Triangle Height Calculator
If you are looking for an easy tool to calculate the height in any triangle, you're in the right place – this triangle height calculator is the tool for you. Whether you are looking for the triangle height formulas for special triangles such as the right, equilateral or isosceles triangle or any scalene triangle, this calculator is a safe bet – it can calculate the heights of the triangle, as well as triangle sides, angles, perimeter, and area. Please don't wait any longer; give it a go!
If you are still wondering about the formula for the height of an equilateral triangle or how to find height without area, keep scrolling, and you'll find the answer.
What is the altitude of a triangle?
Every side of the triangle can be a base, and from every vertex, you can draw the line perpendicular to a line containing the base – that's the triangle's height. Every triangle has three heights, which are also called altitudes. Drawing the height is known as dropping the altitude at that vertex.
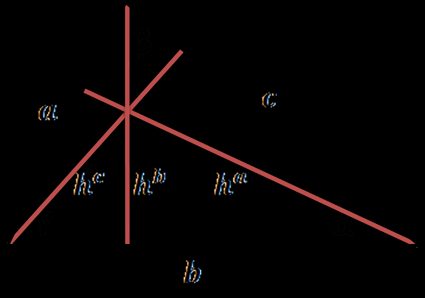
How to find the height of a triangle – formulas
There are many ways to find the height of the triangle. The most popular one is the one using a triangle's area, but many other formulas exist:
-
Given triangle area
The well-known equation for the area of a triangle may be transformed into a formula for the altitude of a right triangle:
-
, where is a base, – height; and
-
So .
But how do you find the height of a triangle without area? The most popular formulas are:
-
-
Given triangle sides
Using an equation called Heron's formula lets you calculate the area, given sides of the triangle. Then, once you know the area, you can use the basic equation to find out what is the altitude of a triangle:
Heron's formula:
Therefore:
You can learn more about this equation in our dedicated Heron's formula calculator.
-
Given two sides and the angle between
Use trigonometry or another formula for the area of a triangle:
(or or if you have different sides given):
If your shape is a special triangle type, scroll down to find the triangle height formulas. Simplified versions of the general equations are easier to remember and calculate.
How to find the height of an equilateral triangle
An equilateral triangle is a triangle with all three sides equal and all three angles equal to . All three heights have the same length that may be calculated from:
- , where is a side of the triangle.
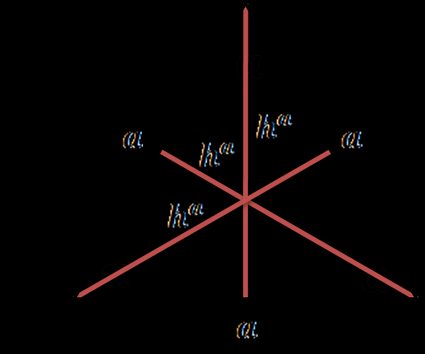
In an equilateral triangle, the altitudes, the angle bisectors, the perpendicular bisectors, and the medians coincide.
If you're interested in the formulas for the area and perimeter, visit our dedicated equilateral triangle calculator.
How to find the height of an isosceles triangle
An isosceles triangle is a triangle with two sides of equal length. There are two different heights of an isosceles triangle; the formula for the one from the apex is:
-
, where is a leg of the triangle, and is a base. The formula is derived from the Pythagorean theorem.
-
The heights from base vertices may be calculated from:
Area formula:
Trigonometry:
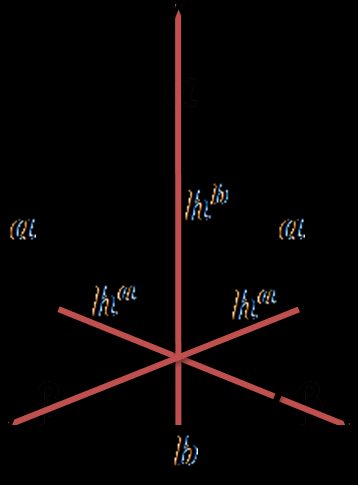
For the area and perimeter formulas of this type of triangle, visit our dedicated isosceles triangle calculator.
How to find the altitude of a right triangle
A right triangle is a triangle with one angle equal to . Two heights are easy to find, as the legs are perpendicular: if the shorter leg is a base, then the longer leg is the altitude (and the other way round). The third altitude of a triangle may be calculated from the formula:

If you're interested in this triangle's area and perimeter equations, look at our right triangle calculator.
How to find the altitude of the triangle with this triangle height calculator?
After reading our explanation, we're pretty sure that now you understand how to find the height of a triangle without the area given or what is the altitude of a triangle. But let's look at a simple example to show you the flexibility of our tool:
- Choose the triangle type. Assume we want to calculate the heights of a scalene triangle, so we don't change the default option.
- Enter the given values. It could be three sides or two sides and an angle. Let's stay with the first option: , , .
- The triangle height calculator displayed all three heights - they are equal to , , and . What is more, the calculator showed us all triangle angles, the area, and the perimeter.
Isn't that awesome?
FAQs
How do you find the height of a triangle if all sides are equal?
To determine the height of an equilateral triangle:
- Write down the side length of your triangle.
- Multiply it by
√3 ≈ 1.73. - Divide the result by
2. - That's it! The result is the height of your triangle!
Are all heights of a triangle equal?
In general no, each height of a triangle may be of a different length. However, if all three heights have equal lengths, then this triangle is equilateral, that is, all of its sides are also equal (but not equal to the heights!).
How do you find the height of a triangle given angles?
You cannot determine the height of a triangle given only the triangle's angles. This is because there are infinitely many triangles with these angles, and the lengths of the altitudes in each of these triangles are different!
How do you find the height of a right triangle?
Each of the perpendicular sides (legs) in a right triangle is its height. To compute the third height h3, go through the area formula:
½ × Leg1 × Leg2 = Area = ½ × Hypotenuse × h3
In consequence:
h3 = Leg1 × Leg2 / Hypotenuse
What is the shortest height of the 3 4 5 triangle?
The answer is 2.4. To arrive at this result, note the area is Area = ½ × 3 × 4 = 6.
On the other hand, Area = ½ × Hypotenuse × Shortest height.
Since Hypotenuse = 5 and Area = 6, we obtain Shortest height = 2 × Area / Hypotenuse = 2 × 6 / 5 = 2.4.