Arcsin Calculator (Inverse Sine)
With this arcsin calculator (or inverse sine calculator) you'll have no issue finding the arcsine in your problem. Simply input the value of sine for the triangle and the angle in question will appear. The only thing you need to remember is the restricted domain of arcsine (−1 ≤ sine ≤ 1). If you're wondering what the arcsine is or what the graph of arcsin x looks like, wait no longer — scroll down and you'll find the answers below! We have also included a short paragraph about arcsine relationships, such as the relationship between arcsines integral and derivative. So, what are you waiting for?
💡 If you have no idea what trigonometry is all about, we recommend you first take a look at Omni's trigonometric functions calculator and, in particular, at the sin calculator.
What is arcsine?
Arcsine is an inverse of the sine function. In other words, it helps to find the angle of a triangle that has a known value of sine:
arcsin(x) = y iff x = sin(y)
As sine's codomain for real numbers is [−1, 1] , we can only calculate arcsine for numbers in that interval. This means that the domain of arcsin (for real results) is -1 ≤ x ≤ 1.
However, as you might (and should!) remember, sine is a periodic function, so there are multiple numbers that have the same sine value. For example sin(0) = 0, but also sin(π) = 0, sin(2π) = 0, sin(-π) = 0 and sin(-326π) = 0. Therefore, if somebody wants to calculate arcsin(0), the answer can be 0, 2π (360°), or -π (-180°), to name a few options! All of them are correct, but we usually only give one number called the principal value.
💡 The usual range of usual principal values is -π/2 ≤ y ≤ π/2
radians that is, -90° ≤ y ≤ 90°.
Arcsin(x) is the most common notation, as sin-1x may lead to confusion (because sin-1x ≠ 1/sin(x) ). The abbreviation asin(x) in usually used in computer programming languages.
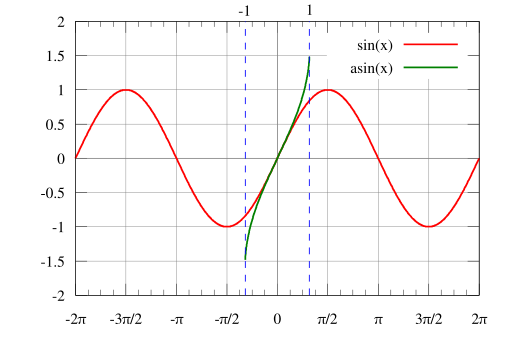
Graph of arcsin x
As the basic function sine is not one-to-one, its domain must be restricted in order to ensure that arcsine is also a function. Usually, the chosen domain is -π/2 ≤ y ≤ π/2. This means that the range of the inverse function will be equal to the range of a principal function; thus, the range of the arcsin function is [−π/2,π/2], and the arcsine domain is between [−1,1]. Below, you can find the graph of arcsin(x), as well as some commonly used arcsine values:
x | arcsin(x) | |
|---|---|---|
deg | rad | |
-1 | -90° | -π/2 |
-√3 / 2 | -60° | -π/3 |
-√2 / 2 | -45° | -π/4 |
-1/2 | -30° | -π/6 |
0 | 0° | 0 |
1/2 | 30° | π/6 |
√2 / 2 | 45° | π/4 |
√3 / 2 | 60° | π/3 |
1 | 90° | π/2 |
And here's how the graph of arcsin x looks like:

Wondering where this graph comes from? It may be found by reflecting a graph of sin(x), between the range of [-π/2 π/2], through the line y = x:
Inverse sine, trigonometric functions, and other relationships
The relationships between the trigonometric functions and arcsine may help you understand the topic even better. A right-angled triangle that has a hypotenuse of length 1 is a good starting point.
Just a quick reminder: for a right-angled triangle, the sine function takes the angle θ and returns the ratio of the opposite/hypotenuse, which is equal to x in our exemplary triangle. The inverse sine function, arcsine, will take the ratio of the opposite/hypotenuse (x) and return the angle, θ. So, knowing that, for our triangle, arcsin(x) = θ we can also write that:
- Sine:
sin(arcsin(x)) = x - Cosine:
cos(arcsin(x)) = √(1-x²) - Tangent:
tan(arcsin(x)) = x / √(1-x²)
Other useful relationships with arcsine are:
arcsin(x) = π/2 − arccos(x)arcsin(-x) = -arcsin(x)
Sometimes, the integral and derivative of arcsin are needed as well:
- integral of arcsin:
∫arcsin(x) dx = x arcsin(x) + √(1 − x²) + C - derivative of arcsin:
d/dx arcsin(x) = 1 / √(1 − x²)where x ≠ -1, 1
Example of how to use the arcsin calculator

Arcsine is a function that is useful, for example, in finding the angle of a right triangle. If you're searching for the angles in a right triangle and you know the side lengths, the well-known Pythagorean theorem wouldn't be so helpful. Finding the angles of a right triangle requires applying arcsine:
- for α:
sin(α) = a / c so α = arcsin(a / c) - for β:
sin(β) = b / c so β = arcsin(b / c)
So let's assume we have two values given in a right triangle, a = 6 and c = 10, and we'd like to find the value of the angle α:
- Input the value you want to find the arcsine of. In our case, it's 6/10. So, you can enter the value as 0.6, but the form 6/10 will also work. Just remember that the value should be between −1 and 1.
- And... that's it! The arcsin calculator did its job, and you've found the arcsine of your value. Now you know that arcsine(6/10) = 36.87°.
🙋 But, teacher, will I use this in real life? For once, yes! Or maybe not, hopefully. When forensic scientists try to reconstruct a crime scene, the arcsin function is of utmost importance: discover why at our angle of impact calculator.
FAQs
What is arcsin(1) in terms of pi?
arcsin(1) = π/2 (= 90°). The arcsin is the inverse function of the sin function. Since sin(π/2) = 1, arcsin(1) = π/2.
Is arcsin the same as sin⁻¹?
Yes, arcsin and sin⁻¹ refer to the inverse of the sin function. In fact, sin⁻¹() is another way to denote the arcsin function. However, arcsin is the more commonly used symbol.
What does it mean to find arcsin?
Finding the arcsin of a value x is to find the angle θ in a right-angled triangle, such that x is the ratio of the side opposite to this angle θ to the triangle's hypotenuse.
How do you calculate arcsin?
The arcsin function is an inverse trigonometric function. To calculate the value arcsin(x), follow these steps:
-
Find a graph of the arcsin function in the range [-1,1].
-
Find the point on the arcsin curve such that its x-coordinate is equal to x.
-
Find the y-coordinate of this point. The value of the y-coordinate is the arcsin(x).
-
Verify with our arcsin calculator.