Complex Number to Polar Form Calculator

This complex number to polar form calculator is here to serve whenever you need to quickly convert a complex number to polar form. Let's briefly recall what the polar form is and how the conversion works so that you know how to do it by hand if you ever face such a challenge.

There are a few ways to represent a given complex number, and the polar form is one of them. You're most probably already familiar with the form z = a + bi, where a and b are the rectangular coordinates.

The polar form uses the fact that z can be identified by two numbers:

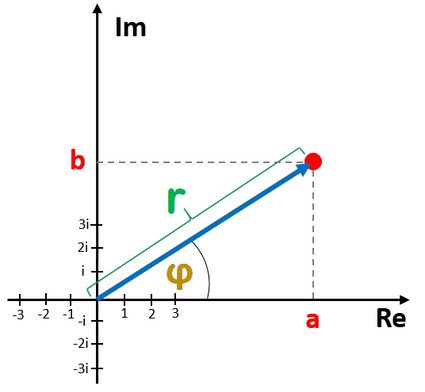
• The distance r from the origin of the plane (i.e., the point (0,0)) to z; and
• The angle φ between the horizontal axis and the radius connecting the origin and z.

We call r the modulus (or the magnitude) and φ the argument of z.

The trigonometric form of a complex number z reads

z = r × [cos(φ) + i × sin(φ)],

where:

• r is the modulus, i.e., the distance from (0,0) to z; and
• φ is the argument, i.e., the angle between the x-axis and the radius between (0,0) and z.

Let us discuss how to convert from a rectangular form complex number to polar form.

To understand how to convert from complex number a + bi to polar form, we need to recall the Pythagorean theorem and some basics of trigonometry.

Look at the figure above and note that

r² = a² + b²

as well as

tan(φ) = b / a.

The first formula tells us how to get r from a and b:

r = √(a² + b²).

Getting φ is slightly more complicated as it is trapped under the tangent function. We need to compute the inverse of the tangent function, that is, the arcus tangent (atan) function:

φ = atan2(b, a).

The mysterious atan2 function is defined simply as atan2(b, a) = arctan(b / a) if a > 0. But if a < 0, then atan(b / a) does not give us the right answer - we must correct it by ±π to end up in the correct quadrant of the plane. The definition of atan2(b, a) provides this correction. Formally, atan2(b, a) is equal to:

• atan(b / a) if a > 0;
• atan(b / a) + π if a < 0 ≤ b;
• atan(b / a) - π if a,b < 0;
• π/2 if `a = 0 < b``;
• -π/2 if b < 0 = a; and
• remains undefined if x = y = 0.

These are exactly the formulas behind Omni's polar form converter.

This tool is really straightforward to use: given a complex number in its rectangular form, so the a + bi form, you need to input a and b into their respective fields.

Our complex number to polar form calculator will immediately display the magnitude r and phase (argument) φ of your number, so that you can write down the polar form r × exp(iφ).

As complex numbers are an essential tool in math and science, the Omni team built a rich collection of tools related to this topic:

• Complex number calculator;
• Imaginary number calculator;
• a+bi form calculator;
• Polar form calculator;
• Multiply complex numbers calculator;
• Divide complex numbers calculator;
• Complex number to trigonometric form calculator;
• Complex number to rectangular form calculator; and
• i calculator.