Imaginary Number Calculator

Our imaginary number calculator is here to help you perform various arithmetic operations on two complex numbers. Are you looking for a simple calculator to add imaginary numbers? Or maybe you're for something more advanced, say, finding the natural logarithm of a complex number. Well, you've come to the perfect imaginary calculator!

Here's a list of operations with complex numbers this calculator can handle:

• Adding and subtracting two imaginary numbers;
• Multiply or divide two complex numbers;
• Raise the first complex number to the power of the second complex number;
• Find the natural log of the first complex number; and
• Find the magnitude and phase of complex numbers.

Before you head off to have fun with our imaginary number calculator, go through the article below to understand what complex numbers are and how to calculate these operations with complex numbers.

Complex numbers are numbers with a real part and an imaginary part. They're of the form:

Where:

• $z$ - Complex number;
• $a,b$ -Real numbers;
• $i$ - Imaginary unit, such that $i^2 = \sqrt{-1}$.

An imaginary number is a complex number whose real part is zero $(\text{Re}(z)=0)$ and whose imaginary part is non-zero $(\text{Im}(z)\neq 0)$.

Apart from the Cartesian form $z = a + ib$, we can express a complex number in the polar form, using its magnitude and phase angle.

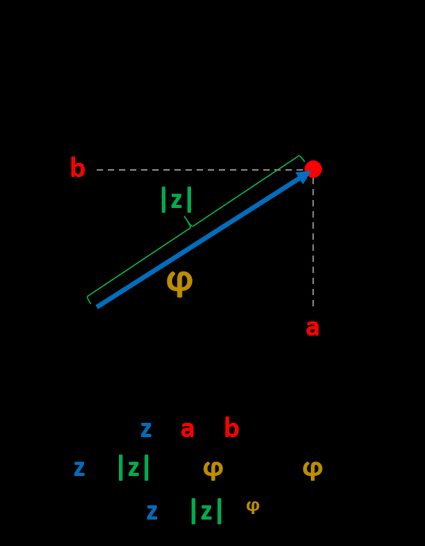
The magnitude $|z|$ (or the absolute value) of a complex number $z$ is given by:

The phase angle $\varphi$ of a complex number $z$ is given by:

The polar form of the complex number $z$ is written as:

Where $e$ is the Euler's number.

Let's briefly discuss how various arithmetic operations are performed on complex numbers. Bear in mind that these operations are valid for purely imaginary numbers too!

Addition and Subtraction

The addition and subtraction of two complex numbers are pretty straightforward. Say we have two complex numbers $z_1 = a + ib$ and $z_2 = c + id$:

Multiplication and division

The multiplication and division of complex numbers may seem slightly more complex (pun unintended!). Consider two complex numbers $z_1 = a + ib$ and $z_2 = c + id$. Their multiplication is given by:

On the other hand, their division is given by:

Power and natural log

Raising one complex number $z_1= a + ib$ to the power of another complex number $z_2 = c + id$ requires you to use the polar form:

You can compute the natural logarithm of a complex number (also known as a complex natural log) using the formula:

Our imaginary number calculator is simple to use:

1. Enter the real and imaginary parts of the a complex number. The imaginary number calculator will immediately tell you this:
   1. Magnitude; and
   2. Phase angle.
2. Enter a second complex number in a similar manner, and the calculator will do the following
   1. The calculator adds the imaginary numbers to give you their sum. Similarly, it'll also generate the difference between the two complex numbers $(z_1-z_2)$.
   2. The calculator multiplies the imaginary numbers to give you their product.
   3. The calculator divides the complex number $(z_1/z_2)$ to give you their quotient.
   4. It will raise the first complex number to the power of the second complex number $z_1^{z_2}$.
   5. Finally, it generates the natural logarithm of the first complex number $\ln(z_1)$.

Check out our tools that deal with similar calculations on complex numbers:

• Complex number calculator;
• a+bi form calculator;
• Divide complex numbers calculator;
• Multiply complex numbers calculator;
• Complex number to polar form calculator;
• Complex number to trigonometric form calculator;
• Complex number to rectangular form calculator;
• i calculator; and
• Polar form calculator.

The natural log of the complex number z = 5 + 7i is 2.152 + 0.951i. To arrive at this answer, follow these steps:

1. Find the magnitude of z = 5 + 7i, to get |z| = √(5²+ 7²) = 8.602.
2. Compute the phase angle of z = 5 + 7i, to get ϕ = tan^-1(7/5) = 0.951 rad.
3. Use the complex natural log formula ln(z) = ln|z| + iϕ to get ln(5+7i) = ln|8.602| + i0.951 = 2.152 + 0.951i.
4. You can verify your result with our imaginary number calculator.

Zero is considered both a real and a complex number. This is because we can express it as 0 = 0 + 0i. Technically, we can express any real number a in the complex form, a = a + 0i.