Complex Number Calculator

Our complex number calculator (also known as an imaginary number calculator) is an excellent tool for solving basic operations with complex numbers. Read on to find the answer to the question: "what is a complex number" learn about the algebraic and polar forms of complex numbers, and master the skills of multiplying and dividing complex numbers.

At the end of this text, you can also find information about the properties of complex numbers (most of which are based on the conjugate or the absolute value of complex numbers) and even some practical applications of them.

To answer the question of what is a complex number, we have first to ask: "What is an imaginary number?". An imaginary number is the square root of a negative number. The basic imaginary number is denoted with the letter $i$ (sometimes $j$ e.g. in electronics), and is defined by:

The definition of a complex number $z$ is the combination of real $a$ and imaginary $b\!\cdot\!i$ parts, so that:

Here, both $a$ and $b$ are classically understood as real numbers. When $b = 0$, the number is purely real, and if $a = 0$, we have a purely imaginary number. You can use this complex number calculator as an imaginary number calculator - just input the real component equal to 0.

Another way to write two parts of a complex number is $\mathrm{Re}$ and $\mathrm{Im}$ so that $\mathrm{Re}(z)=a$, and $\mathrm{Im}(z)=b$. In fact, there are also numbers with more imaginary parts: check our quaternion calculator. Fortunately, we don't have to worry about them here.

The conjugate of a complex number is defined as:

As we can see, the conjugate of a complex number doesn't affect the real part, while the imaginary part has the opposite sign as the original.

Complex numbers have a lot in common with the Cartesian coordinate system because they are pairs of numbers on a Cartesian complex plane. It's helpful to imagine complex numbers as vectors on that complex plane. The formulas which transform complex numbers from Cartesian form to polar form are exactly the same as classical coordinate transformations:

• $|z| = a² + b²$,
• $\tan(\varphi) = \frac{b}{a}$,

where $|z|$ is the modulus/absolute value of the complex number, $\varphi$ is known as an argument or phase (sometimes we use notation $\mathrm{arg}(z) = \varphi$), and $\tan$ is the tangent of the given argument.

Similarly, the length of a vector in the two-dimensional Euclidean plane is the distance between its end and the origin of the coordinate system. The angle $\varphi$ is measured from the X-axis counterclockwise, and it can vary from $0$ to $2\pi$ or from $-\pi$ to $\pi$ (depending on convention since both are equivalent).

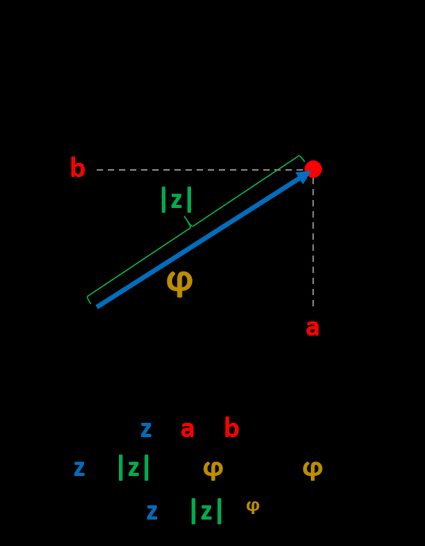
Knowing that we can write any complex number using its polar coordinates on that plane:

• $a = |z| \cdot \cos\varphi$,
• $b = |z| \cdot \sin\varphi$.

Here sin and cos are basic trigonometric functions. We derive these formulas from the relations in the right triangle on the complex plane. In other words, we can write the complex number as: $z = |z| (\cos\varphi + i\cdot\sin\varphi)$.

There is also another way to rewrite this number, using the Euler formula:

$z = |z| \cdot \exp(iφ)$,

where $\exp()$ is an exponent function, the base of which is the number $\mathrm{e}$. Because of the periodicity property, we can see that:

$\exp(i\varphi) = \exp[i(\varphi + 2k\pi)]$,

where $k$ is any integer number.

The polar form of complex numbers is handy in various calculations, including multiplication, division, and even some more sophisticated ones. The exponential form is convenient if you are not proficient enough in trigonometric laws or you just prefer to work with powers.

When performing simple operations with complex numbers, it's helpful to think about them as vectors. Then, it's pretty straightforward to achieve both addition and subtraction of complex numbers.

Let's denote the first number as $F = a + bi$ and the second one as $G = c + di$. Then, the sum of two complex numbers is:

where $\mathrm{Re}(F + G) = a + c$ is the real part of the sum, and $\mathrm{Im}(F + G) = b + d$ is imaginary one.

Analogically, we can find the difference between these numbers:

and now $\mathrm{Re}(F - G) = a - c$, and $\mathrm{Im}(F - G) = b - d$.

Do you remember how to add or subtract two 2D vectors? It's precisely the same as we do it in this complex number calculator - you just need to add (or subtract) each pair of components separately, and that's it!

Now, let's move to something more challenging - we want to find how multiplying complex numbers work. Following with notation from the previous section, we can write:

This time the real part can be written as $\mathrm{Re}(F\!\cdot\!G) = a\!\cdot\!c - b\!\cdot\!d$, and imaginary part as $\mathrm{Im}(F\!\cdot\!G) = a\!\cdot\!d + b\!\cdot\!c$. Note that there is a minus sign in the real part since, at some point, we faced a multiplication of two imaginary numbers $i\!\cdot\!i$, which equals $-1$ by definition.

Multiplying complex numbers isn't that scary. Is it? So what about dividing complex numbers? Let's have a look at calculations with step-by-step hints:

• $F / G = \frac{a + bi}{c + di}$, extend both numerator and denominator by the conjugate of a complex number of the latter.
• $= \frac{(a + bi) \cdot (c - di)}{(c + di) \cdot (c - di)}$, perform standard multiplications.
• $= \frac{a \cdot c - a \cdot d \cdot i + b \cdot c \cdot i - b \cdot d \cdot i \cdot i}{c² - (di)²}$, once again, use the fact that $i\!\cdot\!i = -1$.
• $= \frac{a \cdot c + b \cdot d + (b \cdot c - a \cdot d) \cdot i} {c² + d²}$.

We obtain the following results: $\mathrm{Re}(F / G) = \frac{a \cdot c + b \cdot d}{c² + d²}$, $\mathrm{Im}(F\!\cdot\!G) = \frac{b \cdot c - a \cdot d}{c² + d²}$. Of course, the division is possible only if $G \neq 0$.

We can also consider the operations above in the polar notation, say $F = |z_1|\exp(i\varphi_1)$, $G = |z_2|\exp(i\varphi_2)$. Then, multiplying complex numbers is given by:

and we can see that: $|F\!\cdot\!G| = |z_1\!\cdot\!z_2|$, and $\arg(F\!\cdot\!G) = \varphi_1\!+\!\varphi_2$.

Dividing complex numbers is almost the same with this notation:

rewriting the result as: $|F / G| = |z_1/z_2|$, and $\arg(F / G) = \varphi_1\!-\!\varphi_2$. Using this form, it's clearly visible that the resulting module is the ratio of both numbers' absolute values.

It looks like the second attempt is much simpler; thus sometimes it's worth considering changing the form of our expressions before starting a calculation. We can always come back from polar to algebraic notation. If you don't feel comfortable with it, just use our complex number calculator to ensure the outcome is correct.

We can give a brief overview of how to calculate some more complicated operations with complex numbers. Firstly, let's find the general formula for the complex power of two numbers, given as $F^G$.

• $F^G = (a + bi)^{(c + di)}$ since it isn't obvious how to extend that expression, we can write F in the polar form of complex numbers.
• $= (|z_1|\exp(i\varphi_1))^{(c + di)}$, now the product to any power of a sum is the product of each element to every component separately.
• $= |z_1|^c \cdot \exp(i\varphi_1\!\cdot\!c) \cdot |z_1|^{di} \cdot \exp(-\varphi_1\!\cdot\!d)$, we can use the known property of exponent that is: $x^n = \exp(n\!\cdot\!\ln(x))$, where $\ln$ is the natural logarithm.
• $= |z_1|^c \cdot \exp(-\varphi_1\!\cdot\!d) \cdot \exp[i(\varphi_1\!\cdot\!c + d\!\cdot\!\ln|z_1|)]$.

Then, the absolute value is: $|F^G| = |z_1|^c \cdot \exp(-\varphi_1\!\cdot\!d)$, while the argument is: $\arg(F^G) = \varphi_1c + d\ln|z_1|$. Although we are mixing two different notations, it's fine. We can also change them anyway you like - that's all your choice.

The logarithm of a complex numbers (also known as the complex logarithm) can be worked out the following way:

One critical remark: since the phases $\varphi_1$ and $\varphi_1+2k\pi$ are equivalent, the complex logarithm has an infinite number of solutions, and we can write the general result as: $\ln(|z_1|) + i(\varphi_1+2k\pi)$.

The tool is straightforward to use. All you have to do is write both the real and imaginary parts of two numbers. If a number is purely real or imaginary, set the other component equal to 0. And that's it.

As a result, you will obtain the polar form of complex numbers, the sum, the difference, the product, and the quotient, as well as the first number to the power of the second one and the logarithm of the first number.

There are several properties of complex numbers, including conjugate or the absolute value of complex numbers, which can be handy while calculating some exercises.

1. $\mathrm{Re}(z) = \mathrm{Re}(\bar{z})$;
2. $\mathrm{Im}(z) = -\mathrm{Im}(\bar{z})$;
3. $z \cdot \bar{z} = |z|^2$;
4. $|z_1 + z_2| \le |z_1| + |z_2|$;
5. $|z_1 \cdot z_2| = |z_1| \cdot |z_2|$;
6. $|\frac{z_1}{z_2}| = \frac{|z_1|}{|z_2|}$; and
7. If $z = 0$, then both $a = 0$ and $b = 0$.

Complex numbers are sometimes really helpful with algebraic expressions, especially if they are related to trigonometric functions.

Many physics problems benefit from the power of complex numbers. One of the main fields of complex number usage is the world of wave functions and harmonic motion. Also, we can significantly simplify multiple issues from electronics with complex numbers. You can check how we can do it in practice with the voltage divider calculator.