Voltage Divider Calculator

This is a voltage divider calculator – a comprehensive but simple tool that helps you evaluate the output signal (i.e., voltage) that we obtain in a single voltage divider, often used in voltage regulators.

Read on to learn what is a voltage divider, find out the basic voltage divider formula, and how it extends to various equations for different voltage divider types. Also, learn how it is possible to obtain some fraction of input voltage by applying the voltage divider rule.

Additionally, check out the numerous applications of a voltage divider in basic and incredibly complex systems, and convince yourself that electronic circuits are nothing to worry about!

A simple voltage divider is a part of a linear circuit that changes input voltage ($V_1$) into an output voltage ($V_2$), which is a different value. Since the circuit is a passive one, the ratio $V_2 / V_1$ is never greater than 1. You can see the generic voltage divider in this simple diagram:

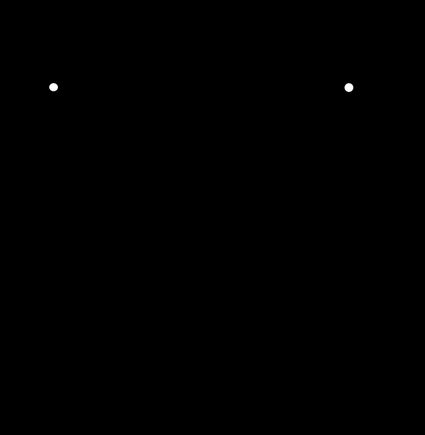
where $Z_1$ and $Z_2$ are some impedances. The impedances can be related to the resistance $R$, the capacitance $C$, or the inductance $L$. We can distinguish a few basic types of voltage dividers for which we can apply the voltage divider rule:

1. Resistive divider, RR;

2. Capacitive divider, CC;

3. Inductive divider, LL;

4. RC and CR dividers (also known as RC, CR filters);

5. RL and LR dividers (also known as RL, LR filters); and

6. CL and LC dividers (also known as CL, LC filters).

The principle behind voltage dividers is that the current passing through several elements connected in series is constant, but the voltage divides somehow between them. We need to apply Ohm's law to our circuit to find the exact values. Before doing that, we must state one crucial point:

RR composition is the only one applicable to DC (direct current) circuits. In these cases, we can treat any impedance as a wire with zero resistivity, and capacitances work as a gap in a circuit, so they have infinite resistance. For the rest, they are all used with AC (alternating current) circuits, and the voltage divider rule is applicable for the maximum value of the potential difference. It may also be helpful to find the phase shift for these voltages.

The general voltage divider equation (or formula) for impedances is as follows:

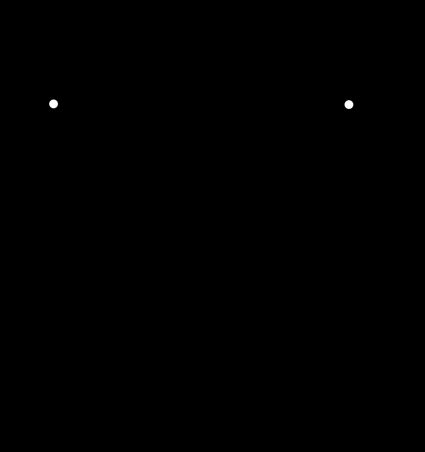
A reminder: in general, $V_1$ and $V_2$ correspond to the amplitudes of signals, e.g., sinusoidal ones.

If we are considering only resistances, the voltage divider formula naturally changes to:

Since the resistance doesn't affect the signal phase, the formula is the same for both AC and DC cases. We compare voltage values at a given moment. As mentioned before, we consider the remaining kinds of dividers for AC circuits, so let's take a look at some examples.

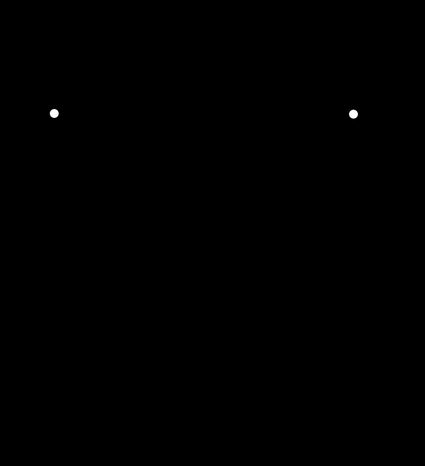
For a CC divider, we need to use the impedances of capacitors: $Z\!=\!\frac{1}{j\omega C}$, where $j$ stands for an imaginary number, and $\omega$ is the angular frequency of alternating voltage. Substituting the original voltage divider equation with this expression, we obtain:

and multiplying each term by $j\omega C_1C_2$ the result is:

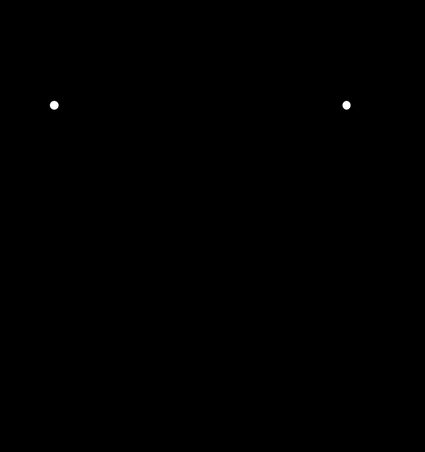
We can proceed with a similar procedure for LL dividers, where $Z = j\omega L$. This time the outcome voltage is:

Dividing numerator and denominator by $j\omega$ the final formula is:

In both cases, the output voltage is in phase with respect to the input phase.

Voltage divider circuits consisting of more than one type of element are not as simple to evaluate as the previous examples. We have to deal with complex number algebra, but trust us, it looks more frightening than it actually is.

For an RC divider, we can extend the voltage divider formula to:

The result is a complex number, so in order to estimate the amplitude of the output voltage, we have to find its module:

If the frequency increases, the output amplitude of the voltage decreases, which is why we call this circuit a low pass filter. We can work out the phase shift can as the inverse tangent of the imaginary part divided by the real part of our complex number:

Analogically, we can find the amplitude and the phase shift for the CR circuit. The first step is to evaluate the general formula for output voltage:

We can work out its amplitude as:

and the phase shift is given as:

This time we can see that if the frequency tends towards 0, the same happens to the amplitude of $V_2$, and, for high values of $\omega$, it remains the same as the input voltage. The conclusion is that CR can be treated as a high pass filter.

Circuits containing resistant and inductive elements aren't much different from RC and CR ones when it comes to calculations. Still, it's worth repeating each step to realize all the subtle differences.

In the case of the RL filter, we can start, as usual, with the general formula of the voltage divider:

To find the amplitude of the output voltage, we need to estimate the module of that value:

and its phase shift is:

For an LR divider, we just replace these elements, so the voltage divider equation results in the following:

Once again, we can determine the amplitude of the output voltage and the phase shift:

Take a look at the outcomes; the $V_2$ amplitude for the RL filter is very similar to CR, and that of LR resembles the voltage amplitude of RC. So do their phase shifts. It's a very valuable outcome because it turns out that we can use RC and RL filters interchangeably when designed in an appropriate configuration, and the values of conductance and inductance are adequately adjusted. It's especially useful for circuits that have to be resized to the nanometer scale since applying really small capacitors is much easier than creating tiny coils.

Anyway, suppose you have trouble calculating the output signal's properties. In that case, you can always come back to these chapters or try our voltage divider calculator! Choose a suitable option, and the result will be displayed instantly.

We described several passive filters above, but we can also apply the voltage divider rule with active ones.

We could perform the same calculations for CL and LC systems. However, some ridiculous outcomes may occur if we simply apply the voltage divider rule. We can cause the amplitude of the output voltage can go into infinity! This outcome is caused by the fact that the connected LC elements are sometimes called resonant circuits. We use them for generating and receiving radio waves, which is most efficient at a resonant frequency, given as:

In a more realistic picture, we have to consider also some non-zero resistance, so the problem of the resonant circuits is described in the RLC circuit calculator.

What we have already done shows how voltage dividers work for the simplest systems possible. You can obviously imagine that they are used practically nowhere in real life, and generally, more sophisticated circuits are applied.

However, all the results obtained above can be helpful while simplifying more complex ones. For instance, whenever you can spot resistors in either series or juxtaposed parallel, you can treat them as a single resistance. Similarly, capacitors and solenoids work in much the same way. We evaluate mixed components in practically the same way, but we have to take into account impedances $Z$ instead of $R$, $C$, or $L$.

Here are a few applications of voltage dividers:

1. One of the most commonly used devices which works thanks to the voltage divider concept is a potentiometer. Another word describing this element is a rheostat. They are usually made out of only resistive components. We can distinguish between analog and digital ones, but, in any case, we can set the resistance with high precision. Some of the most popular types of potentiometers are slide pots, trimpots, or thumb pots, which vary by size and structure. The critical element is a sliding contact, adjusting the output resistance possible.

2. High voltage measurement devices – It turns out that it is possible to measure high voltages even if the direct measurement can be destructive for the device. In that case, it's convenient to use the voltage divider to lower the voltage to a safe region. For exceptionally high voltages (let's say above 100 kV), it is better to use capacitive instead of resistive ones.

3. Finding an unknown resistance – Is it possible to find some unknown resistance if you only have a voltage source and another resistor with known resistance? You're lucky if you can read its color code, but what if there isn't one? Well, you can just create a simple circuit with both resistors arranged in series, set an input voltage, and measure the voltage over the desired resistor. Afterward, just insert all these values into the voltage divider calculator, and that's it – the mystery is revealed. You can always transform the general voltage divider equation to find $R₂$ as an unknown parameter:

Some of you may be wondering why people measure an unknown resistance with a voltage divider when they can simply read the value of amperage that flows through the resistor when an external voltage is applied – just a simple Ohm's law. Well, in general, there should be no significant difference between these methods, but we must be aware that the resistance of the vast majority of materials is temperature-dependent. Even worse, these dependencies differ for metals, semiconductors, or insulators.

Considering metals, their resistance increases with the temperature rise, so to define the resistance at some standardized temperature, e.g., T = 25 °C, we have to find the material's thermal coefficient (TCR). This requires precisely measuring the ambient temperature and carrying out some calculations, all while hoping we didn't make any mistakes in the meantime. However, we can do it in a much simpler way! As you may have guessed, you could use a simple voltage divider!

In the basic version, we have two resistors, and if they are made of the same material, it means their temperature dependencies of resistance are roughly the same. No matter how big a temperature difference, these resistances change at approximately the same percentage, say 5%, for every 20°C. But, since, in general, the voltage divider formula has a ratio of impedances, any relative change will cancel, and the output voltage should be temperature independent (or at least its impact ought to be significantly reduced). Moreover, if we look at the equation from the previous section, we'll obtain a value of resistance that is the same as the first one at a given temperature – no further calculations are needed!

Secondly, it's convenient to use voltage dividers when designing some complex electrical circuits. Instead of using multiple distinct voltage sources, each producing a different potential in the system, we can implement a single source and apply as many voltage dividers as we need.

On the other hand, we have to be aware of the fact that the longer the wires in our circuit are, the more likely a voltage drop is. Well, it's nowhere near the odds of that for long industrial cables, but still, if we need to make some really precise measurements, that factor should be taken into account and ideally reduced as much as possible.

So far, we've focused on processing a signal – basically, on voltage changes. Still, we can use a similar concept, looking at the problem from another perspective – a current divider. You can find a more detailed explanation using our current divider calculator.

The idea is almost the same, but instead of dividing input voltage into smaller fractions, we want to divide the initial amperage and get some specific value as the output. There are only a few differences: firstly, we need a current source instead of a voltage one. Secondly, all impedances (in a simple case, two, as usual) must be arranged in parallel, not in series. Actually, these are all crucial differences. With this circuit, we can use Ohm's law once again. The resulting formula is:

We can spot an interesting and valuable property. For a voltage divider, the higher the output resistance, the bigger the output voltage, while for a current divider, the outcome behaves the other way around.

Similarly, we can produce different types of current dividers, including coils and capacitors, and all of these are applicable for alternating current. In contrast, for direct current, only the composition of resistors works. Generally, it is possible to evaluate both the amplitude and the phase shift of a flowing current.

After reading the step-by-step solutions from this voltage divider calculator, we are sure that it won't be any problem for you to perform similar calculations.